über 250 kostenlose
Abituraufgaben
Lösung als Video
und ausformuliert
Alle Lösungen von
erfahrenen Lehrern
Abitur 2019 Mathematik Infinitesimalrechnung I
Teilaufgabe Teil A 1 (5 BE)
Gegeben ist die Funktion mit Definitionsbereich .
Bestimmen Sie Lage und Art des Extrempunkts des Graphen von .
Bestimmen Sie Lage und Art des Extrempunkts des Graphen von .
| Gegeben ist die in definierte Funktion , die die Nullstellen und hat. Abbildung 1 zeigt den Graphen von , der symmetrisch bezüglich der y-Achse ist. Weiterhin ist die Gerade mit der Gleichung gegeben. | 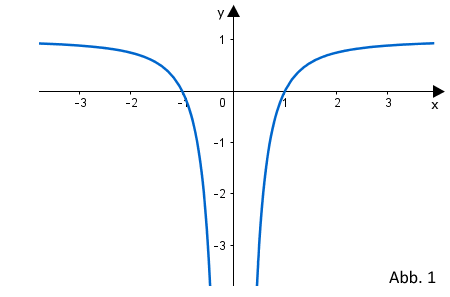 |
Teilaufgabe Teil A 2a (1 BE)
Zeigen Sie, dass einer der Punkte, in denen den Graphen von schneidet, die x-Koordinate hat.
Teilaufgabe Teil A 2b (4 BE)
Bestimmen Sie rechnerisch den Inhalt der Fläche, die der Graph von , die x-Achse und die Gerade einschließen.
| Die nebenstehende Abbildung 2 zeigt den Graphen einer Funktion . | 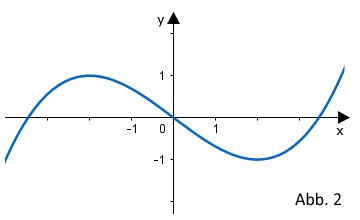 |
Teilaufgabe Teil A 3a (3 BE)
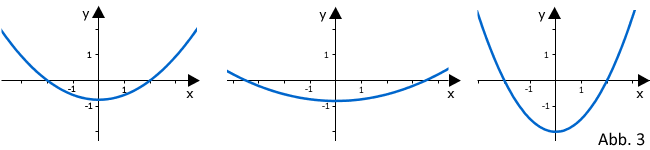
Einer der folgenden Graphen I, II und III gehört zur ersten Ableitungsfunktion von . Geben Sie diesen Graphen an. Begründen Sie, dass die beiden anderen Graphen dafür nicht infrage kommen.

Teilaufgabe Teil A 3b (2 BE)
Die Funktion ist eine Stammfunktion von . Geben Sie das Monotonieverhalten von im Intervall an. Begründen Sie Ihre Angabe.
Teilaufgabe Teil A 4a (3 BE)
Betrachtet wird eine Schar von Funktionen mit , die sich nur in ihren jeweiligen Definitionsbereichen unterscheiden.
Es gilt mit .
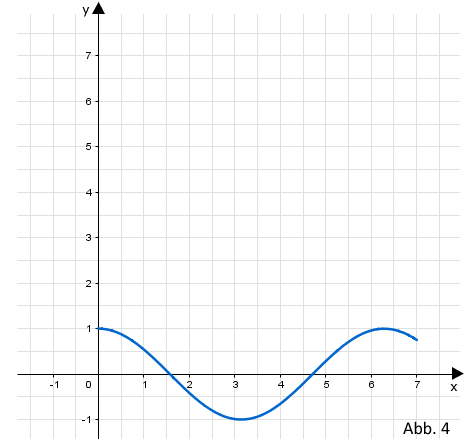
Abbildung 4 zeigt den Graphen der Funktion . Geben Sie den größtmöglichen Wert von an, sodass die zugehörige Funktion umkehrbar ist. Zeichnen Sie für diesen Wert von den Graphen der Umkehrfunktion von in Abbildung 4 ein und berücksichtigen Sie dabei insbesondere den Schnittpunkt der Graphen von Funktion und Umkehrfunktion.
Es gilt mit .
Abbildung 4 zeigt den Graphen der Funktion . Geben Sie den größtmöglichen Wert von an, sodass die zugehörige Funktion umkehrbar ist. Zeichnen Sie für diesen Wert von den Graphen der Umkehrfunktion von in Abbildung 4 ein und berücksichtigen Sie dabei insbesondere den Schnittpunkt der Graphen von Funktion und Umkehrfunktion.

Teilaufgabe Teil A 4b (2 BE)
Geben Sie den Term einer in definierten und umkehrbaren Funktion an, die folgende Bedingung erfüllt: Der Graph von und der Graph der Umkehrfunktion von haben keinen gemeinsamen Punkt.
Gegeben ist die Funktion mit maximalem Definitionsbereich . Der Graph von wird mit bezeichnet.
Teilaufgabe Teil B 1a (3 BE)
Zeigen Sie, dass ist, und geben Sie das Verhalten von an den Grenzen des Definitionsbereichs an.
Teilaufgabe Teil B 1b (2 BE)
Berechnen Sie die Nullstelle von .
Teilaufgabe Teil B 1c (5 BE)
Beschreiben Sie, wie schrittweise aus dem Graphen der in definierten Funktion hervorgeht. Erklären Sie damit das Monotonieverhalten von .
Teilaufgabe Teil B 1d (4 BE)
Zeigen Sie, dass mit Definitionsbereich eine Stammfunktion von ist, und bestimmen Sie den Term der Stammfunktion von , die bei eine Nullstelle hat.
Abbildung 1 zeigt ein Hinderniselement in einem Skate-Park.
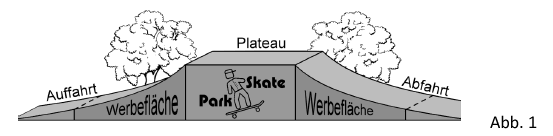
Die Auffahrt des symmetrischen Hinderniselements geht in ein horizontal verlaufendes Plateau über, an das sich die Abfahrt anschließt. Die vordere und die hintere Seitenfläche verlaufen senkrecht zum horizontalen Untergrund. Um die vordere Seitenfläche mathematisch beschreiben zu können, wird ein kartesisches Koordinatensystem so gewählt, dass die x-Achse die untere Begrenzung und die y-Achse die Symmetrieachse der betrachteten Fläche darstellt. Das Plateau erstreckt sich im Modell im Bereich . Die Profillinie der Abfahrt wird für durch den Graphen der in Aufgabe 1 untersuchten Funktion beschrieben (vgl. Abbildung 2). Dabei entspricht eine Längeneinheit im Koordinatensystem einem Meter in der Realität.
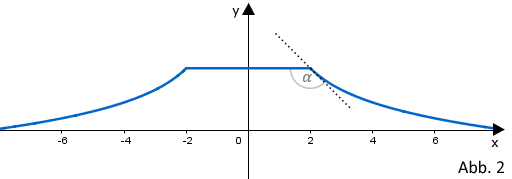

Die Auffahrt des symmetrischen Hinderniselements geht in ein horizontal verlaufendes Plateau über, an das sich die Abfahrt anschließt. Die vordere und die hintere Seitenfläche verlaufen senkrecht zum horizontalen Untergrund. Um die vordere Seitenfläche mathematisch beschreiben zu können, wird ein kartesisches Koordinatensystem so gewählt, dass die x-Achse die untere Begrenzung und die y-Achse die Symmetrieachse der betrachteten Fläche darstellt. Das Plateau erstreckt sich im Modell im Bereich . Die Profillinie der Abfahrt wird für durch den Graphen der in Aufgabe 1 untersuchten Funktion beschrieben (vgl. Abbildung 2). Dabei entspricht eine Längeneinheit im Koordinatensystem einem Meter in der Realität.

Teilaufgabe Teil B 2a (2 BE)
Erläutern Sie die Bedeutung des Funktionswerts im Sachzusammenhang und geben Sie den Term der Funktion an, deren Graph für die Profillinie der Auffahrt im Modell beschreibt.
Teilaufgabe Teil B 2b (5 BE)
Berechnen Sie die Stelle im Intervall , an der die lokale Änderungsrate von gleich der mittleren Änderungsrate in diesem Intervall ist.
Teilaufgabe Teil B 2c (3 BE)
Der in Aufgabe 2b rechnerisch ermittelte Wert könnte alternativ auch ohne Rechnung näherungsweise mithilfe von Abbildung 2 bestimmt werden. Erläutern Sie, wie Sie dabei vorgehen würden.
Teilaufgabe Teil B 2d (2 BE)
Berechnen Sie auf der Grundlage des Modells die Größe des Winkels , den das Plateau und die Fahrbahn an der Kante zur Abfahrt einschließen (vgl. Abbildung 2).
Teilaufgabe Teil B 2e (3 BE)
Die vordere Seitenfläche des Hinderniselements wird in Teilbereichen der Auf- und Abfahrt als Werbefläche verwendet (vgl. Abbildung 1). Im Modell handelt es sich um zwei Flächenstücke, nämlich um die Fläche zwischen und der x-Achse im Bereich sowie die dazu symmetrische Fläche im II. Quadranten. Berechnen Sie unter Verwendung der in Aufgabe 1d angegebenen Stammfunktion , wie viele Quadratmeter als Werbefläche zur Verfügung stehen.
Betrachtet wird die Schar der in definierten Funktionen mit und den zugehörigen Graphen . Für jedes besitzt der Graph genau einen Wendepunkt .
Teilaufgabe Teil B 3a (2 BE)
Geben Sie das Verhalten von an den Grenzen des Definitionsbereichs in Abhängigkeit von an.
Teilaufgabe Teil B 3b (3 BE)
Bestimmen Sie die x-Koordinate von in Abhängigkeit von .
(zur Kontrolle: )
(zur Kontrolle: )
Teilaufgabe Teil B 3c (4 BE)
Bestimmen Sie den Wert von so, dass der zugehörige Wendepunkt auf der y-Achse liegt. Zeigen Sie, dass in diesem Fall der Punkt im Koordinatenursprung liegt und die Wendetangente, d. h. die Tangente an im Punkt , die Steigung 9 hat.
Teilaufgabe Teil B 3d (2 BE)
Für den in Aufgabe 3c bestimmten Wert von zeigt Abbildung 3 den zugehörigen Graphen mit seiner Wendetangente. In diesem Koordinatensystem sind die beiden Achsen unterschiedlich skaliert.
Bestimmen Sie die fehlenden Zahlenwerte an den Markierungsstrichen der y-Achse mithilfe eines geeigneten Steigungsdreiecks an der Wendetangente und tragen Sie die Zahlenwerte in Abbildung 3 ein.
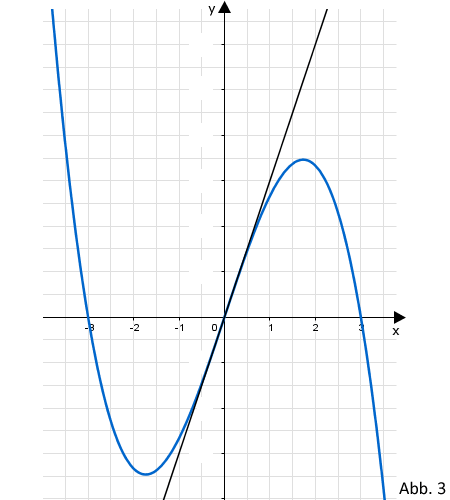
Bestimmen Sie die fehlenden Zahlenwerte an den Markierungsstrichen der y-Achse mithilfe eines geeigneten Steigungsdreiecks an der Wendetangente und tragen Sie die Zahlenwerte in Abbildung 3 ein.

Lösungen zu:
Tipp:
Arbeite frühzeitig mit der Merkhilfe Mathematik,
die als Hilfsmittel im Abitur zugelassen ist.
die als Hilfsmittel im Abitur zugelassen ist.
Feedback:
Du hast einen Fehler gefunden oder hast Anregungen zur Internetseite?








