Abitur 2021 Mathematik Infinitesimalrechnung II

Gegeben ist die Funktion

f

mit

f (x) = \sqrt{x - 2} + 1

und maximalem Definitionsbereich.

Teilaufgabe Teil A 1a (3 BE)

Zeichnen Sie den Graphen von

f

im Bereich

2 \leq x \leq 11

in ein Koordinatensystem.

Teilaufgabe Teil A 1b (3 BE)

Berechnen Sie den Wert des Integrals

\int_{2}^{3} f (x) dx

Geben Sie jeweils den Term einer in

ℝ

definierten Funktion an, die die angegebene Wertemenge

W

hat.

Teilaufgabe Teil A 2a (2 BE)

W =] - \infty; 1]

Teilaufgabe Teil A 2b (2 BE)

W =] 3; + \infty [

Teilaufgabe Teil A 3a (2 BE)

Betrachtet werden eine in

ℝ

definierte ganzrationale Funktion

p

und der Punkt

Q (2 | p (2))

.

Beschreiben Sie, wie man rechnerisch die Gleichung der Tangente an den Graphen von

p

im Punkt

Q

ermitteln kann.

Teilaufgabe Teil A 3b (3 BE)

Gegeben ist eine in

ℝ

definierte Funktion

h : x \mapsto a x^{2} + c

mit

a, c \in ℝ

, deren Graph im Punkt

N (1 | 0)

die Tangente mit der Gleichung

y = - x + 1

besitzt. Bestimmen Sie

a

und

c

Die Abbildung zeigt den Graphen

G_{f}

einer in

ℝ

definierten Funktion

f

G_{f}

ist streng monoton fallend und schneidet die x-Achse im Punkt

(1 | 0)

.
Betrachtet wird ferner die Funktion

g

mit

g (x) = \frac{1}{f (x)}

und maximalem Definitionsbereich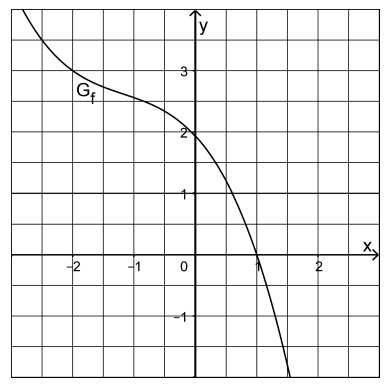

D_{g}

Teilaufgabe Teil A 4a (2 BE)

Begründen Sie, dass

x = 1

nicht in

D_{g}

enthalten ist, und geben Sie den Funktionswert

g (- 2)

an.

Teilaufgabe Teil A 4b (3 BE)

Ermitteln Sie mithilfe der Abbildung die x-Koordinaten der Schnittpunkte der Graphen von

f

und

g

Gegeben ist die in

ℝ

definierte Funktion

f : x \mapsto (1 - x^{2}) \cdot e^{- x}

. Die Abbildung zeigt den Graphen

G_{f}

von

f

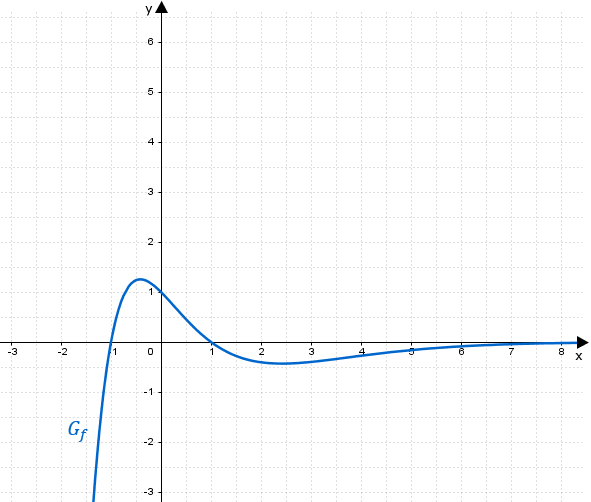
Teilaufgabe Teil B 1a (2 BE)

Zeigen Sie, dass

f

genau zwei Nullstellen besitzt.

Teilaufgabe Teil B 1b (4 BE)

Bestimmen Sie rechnerisch die x-Koordinaten der beiden Extrempunkte von

G_{f}

.

(zur Kontrolle:

f^{'} (x) = (x^{2} - 2 x - 1) \cdot e^{- x}

)

Teilaufgabe Teil B 1c (4 BE)

Ermitteln Sie anhand der Abbildung einen Näherungswert für das Integral

\int_{- 1}^{4} f (x) dx

Die in

ℝ

definierte Funktion

F

ist diejenige Stammfunktion von

f

, deren Graph durch den Punkt

T (- 1 | 2)

verläuft.

Teilaufgabe Teil B 1d (2 BE)

Begründen Sie mithilfe der Abbildung, dass der Graph von

F

im Punkt

T

einen Tiefpunkt besitzt.

Teilaufgabe Teil B 1e (3 BE)

Skizzieren Sie in der Abbildung den Graphen von

F

. Berücksichtigen Sie dabei insbesondere, dass

F (1) \approx 3, 5

und

lim_{x \to + \infty} F (x) = 2

gilt.

Teilaufgabe Teil B 1f (2 BE)

Deuten Sie die Aussage

F (2, 5) - F (0) \approx 0

in Bezug auf

G_{f}

geometrisch.

Betrachtet wird nun die Schar der in

ℝ

definierten Funktionen

h_{k} : x \mapsto (1 - k x^{2}) \cdot e^{- x}

mit

k \in ℝ

. Der Graph von

h_{k}

wird mit

G_{k}

bezeichnet.
Für

k = 1

ergibt sich die bisher betrachtete Funktion

f

Teilaufgabe Teil B 1g (2 BE)

Geben Sie in Abhängigkeit von

k

die Anzahl der Nullstellen von

h_{k}

an.

Teilaufgabe Teil B 1h (3 BE)

Für einen bestimmten Wert von

k

besitzt

G_{k}

zwei Schnittpunkte mit der x-Achse, die voneinander den Abstand 4 haben. Berechnen Sie diesen Wert.

Teilaufgabe Teil B 1i (2 BE)

Beurteilen Sie, ob es einen Wert von

k

gibt, sodass

G_{k}

und

G_{f}

bezüglich der x-Achse symmetrisch zueinander liegen.

Betrachtet wird die in

ℝ

definierte Funktion

g : x \mapsto \frac{e^{x}}{e^{x} + 1}

. Ihr Graph wird mit

G_{g}

bezeichnet.

Teilaufgabe Teil B 2a (5 BE)

Zeigen Sie, dass

g

streng monoton zunehmend ist und die Wertemenge

] 0; 1 [

besitzt.

(zur Kontrolle:

g^{'} (x) = \frac{e^{x}}{{(e^{x} + 1)}^{2}}

)

Teilaufgabe Teil B 2b (3 BE)

Geben Sie

g^{'} (0)

an und zeichnen Sie

G_{g}

im Bereich

- 4 \leq x \leq 4

unter Berücksichtigung der bisherigen Ergebnisse und der Tatsache, dass

G_{g}

W (0 | g (0))

seinen einzigen Wendepunkt hat, in ein Koordinatensystem ein.

Teilaufgabe Teil B 2c (2 BE)

Der Graph der Funktion

g^{*}

geht aus

G_{g}

durch Strecken und Verschieben hervor. Die Wertemenge von

g^{*}

ist

] - 1; 1 [

. Geben Sie einen möglichen Funktionsterm für

g^{*}

an.

Teilaufgabe Teil B 2d (6 BE)

Es wird das Flächenstück zwischen

G_{g}

und der x-Achse im Bereich

- \ln 3 \leq x \leq b

mit

b \in ℝ^{+}

betrachtet. Bestimmen Sie den Wert von

b

so, dass die y-Achse dieses Flächenstück halbiert.

Alle Abituraufgaben

Lösungen zu:

Teilaufgabe Teil A 1a

Teilaufgabe Teil A 1b

Teilaufgabe Teil A 2a

Teilaufgabe Teil A 2b

Teilaufgabe Teil A 3a

Teilaufgabe Teil A 3b

Teilaufgabe Teil A 4a

Teilaufgabe Teil A 4b

Teilaufgabe Teil B 1a

Teilaufgabe Teil B 1b

Teilaufgabe Teil B 1c

Teilaufgabe Teil B 1d

Teilaufgabe Teil B 1e

Teilaufgabe Teil B 1f

Teilaufgabe Teil B 1g

Teilaufgabe Teil B 1h

Teilaufgabe Teil B 1i

Teilaufgabe Teil B 2a

Teilaufgabe Teil B 2b

Teilaufgabe Teil B 2c

Teilaufgabe Teil B 2d

Lösung als Video:

Themen-Übersicht

Tipp:

Arbeite frühzeitig mit der Merkhilfe Mathematik,
die als Hilfsmittel im Abitur zugelassen ist.

Feedback:

Du hast einen Fehler gefunden oder hast Anregungen zur Internetseite?

Teile uns Dein Feedback mit!