über 250 kostenlose
Abituraufgaben
Lösung als Video
und ausformuliert
Alle Lösungen von
erfahrenen Lehrern
Abitur 2016 Mathematik Infinitesimalrechnung I
Gegeben ist die Funktion mit maximaler Definitionsmenge .
Teilaufgabe Teil A 1a (2 BE)
Bestimmen Sie .
Teilaufgabe Teil A 1b (2 BE)
Bestimmen Sie den Wert mit .
Teilaufgabe Teil A 2 (3 BE)
Zeigen Sie, dass der Graph der in definierten Funktion punktsymmetrisch bezüglich des Koordinatenursprungs ist, und geben Sie den Wert des Integrals an.
Teilaufgabe Teil A 3 (3 BE)
Skizzieren Sie im Bereich den Graphen einer in definierten Funktion mit den folgenden Eigenschaften:
- ist nur an der Stelle nicht differenzierbar.
- und für die Ableitung von gilt: .
- Der Graph von ist im Bereich linksgekrümmt.
Gegeben ist eine in definierte ganzrationale Funktion dritten Grades, deren Graph an der Stelle einen Hochpunkt und an der Stelle einen Tiefpunkt besitzt.
Teilaufgabe Teil A 4a (3 BE)
Begründen Sie, dass der Graph der Ableitungsfunktion von eine Parabel ist, welche die -Achse in den Punkten und schneidet und nach oben geöffnet ist.
Teilaufgabe Teil A 4b (2 BE)
Begründen Sie, dass die -Koordinate des Wendepunkts von ist.
Die Abbildung zeigt den Graphen der in definierten Funktion .
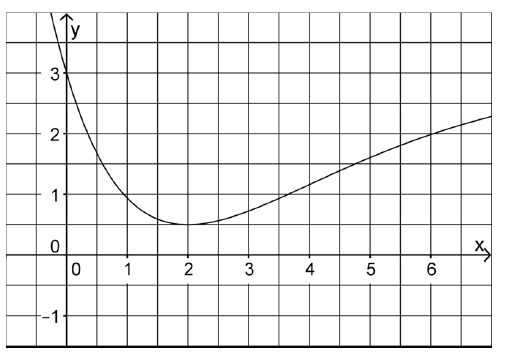

Teilaufgabe Teil A 5a (2 BE)
Bestimmen Sie mithilfe der Abbildung einen Näherungswert für .
Die Funktion ist die in definierte Stammfunktion von mit .
Teilaufgabe Teil A 5b (1 BE)
Geben Sie mithilfe der Abbildung einen Näherungswert für die Ableitung von an der Stelle an.
Teilaufgabe Teil A 5c (2 BE)
Zeigen Sie, dass mit gilt.
Gegeben ist die in definierte Funktion Der Graph von wird mit bezeichnet.
Teilaufgabe Teil B 1a (2 BE)
Bestimmen Sie die Koordinaten des Schnittpunkts von mit der y-Achse und begründen Sie, dass oberhalb der x-Achse verläuft.
Teilaufgabe Teil B 1b (3 BE)
Ermitteln Sie das Symmetrieverhalten von sowie das Verhalten von für und für .
Teilaufgabe Teil B 1c (4 BE)
Zeigen Sie, dass für die zweite Ableitung von die Beziehung für gilt. Weisen Sie nach, dass linksgekrümmt ist.
[Zur Kontrolle: ]
[Zur Kontrolle: ]
Teilaufgabe Teil B 1d (3 BE)
Bestimmen Sie Lage und Art des Extrempunkts von .
Teilaufgabe Teil B 1e (3 BE)
Berechnen Sie die Steigung der Tangente an im Punkt auf eine Dezimale genau. Zeichnen Sie den Punkt und die Gerade in ein Koordinatensystem ein (Platzbedarf im Hinblick auf das Folgende: , ).
Teilaufgabe Teil B 1f (4 BE)
Berechnen Sie , im Hinblick auf eine der folgenden Aufgaben auf zwei Dezimalen genau, und zeichnen Sie unter Berücksichtigung der bisherigen Ergebnisse im Bereich in das Koordinatensystem aus Aufgabe 1e ein.
Teilaufgabe Teil B 1g (3 BE)
Zeigen Sie durch Rechnung, dass für die Beziehung gilt.
Die als Kurvenlänge bezeichnete Länge des Funktionsgraphen von zwischen den Punkten und mit lässt sich mithilfe der Formel berechnen.
Teilaufgabe Teil B 1h (4 BE)
Bestimmen Sie mithilfe der Beziehung aus Aufgabe 1g die Kurvenlänge des Graphen von zwischen den Punkten und mit .
[Ergebnis: ]
[Ergebnis: ]
| Die Enden eines Seils werden an zwei vertikalen Masten, die 8,00 m voneinander entfernt sind, in gleicher Höhe über dem Erdboden befestigt. Der Graph aus Aufgabe 1 beschreibt im Bereich modellhaft den Verlauf des Seils, wobei die Fußpunkte und der Masten durch die Punkte bzw. dargestellt werden (vgl. Abbildung). Eine Längeneinheit im Koordinatensystem entspricht einem Meter in der Realität. | 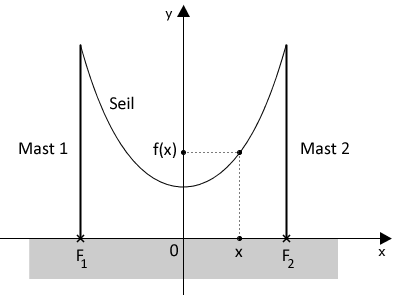 |
Teilaufgabe Teil B 2a (2 BE)
Der Höhenunterschied zwischen den Aufhängepunkten und dem tiefsten Punkt des Seils wird als Durchhang bezeichnet. Berechnen Sie auf der Grundlage des Modells den Durchhang des Seils auf Zentimeter genau.
Teilaufgabe Teil B 2b (5 BE)
Berechnen Sie auf der Grundlage des Modells die Größe des Winkels, den das Seil mit Mast 2 im Aufhängepunkt einschließt, sowie mithilfe der Kurvenlänge aus Aufgabe 1h die Länge des zwischen den Masten hängenden Seils auf Zentimeter genau.
Der Graph von soll durch eine Parabel näherungsweise dargestellt werden. Dazu wird die in definierte quadratische Funktion betrachtet, deren Graph den Scheitelpunkt hat und durch den Punkt verläuft.
Teilaufgabe Teil B 2c (4 BE)
Ermitteln Sie den Term der Funktion , ohne dabei zu runden.
Teilaufgabe Teil B 2d (3 BE)
Für jedes wird der Abstand der vertikal übereinander liegenden Punkte und der Graphen von bzw. betrachtet, wobei in diesem Bereich gilt. Der größte dieser Abstände ist ein Maß dafür, wie gut die Parabel den Graphen im Bereich annähert. Beschreiben Sie die wesentlichen Schritte, mithilfe derer man diesen größten Abstand rechnerisch bestimmen kann.
Lösungen zu:
Tipp:
Arbeite frühzeitig mit der Merkhilfe Mathematik,
die als Hilfsmittel im Abitur zugelassen ist.
die als Hilfsmittel im Abitur zugelassen ist.
Feedback:
Du hast einen Fehler gefunden oder hast Anregungen zur Internetseite?








