über 250 kostenlose
Abituraufgaben
Lösung als Video
und ausformuliert
Alle Lösungen von
erfahrenen Lehrern
 
 
 
 
Lösung Abitur Bayern 2014 Mathematik Analytische Geometrie V


 
Teilaufgabe Teil B c  (3 BE)
Der einfallende Lichtstrahl wird in demjenigen Punkt des Spiegels reflektiert, der im Modell durch den Punkt R dargestellt wird. Der reflektierte Lichtstrahl geht für einen Beobachter scheinbar von einer Lichtquelle aus, deren Position im Modell durch den Punkt Q ( 0 | 0 | 1 ) beschrieben wird (vgl. Abbildung).

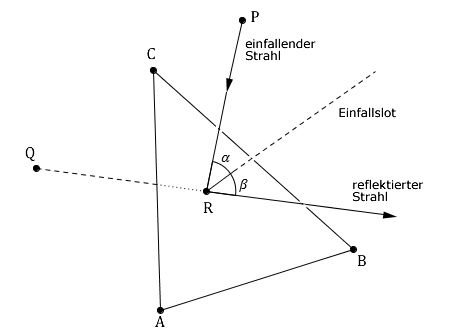
Zeigen Sie, dass die Punkte P und Q bezüglich der Ebene E symmetrisch sind.
 
Lösung zu Teilaufgabe Teil B c

Mittelpunkt einer Strecke



P ( 2 | 2 | 3 ) ; Q ( 0 | 0 | 1 )

Mittelpunkt M der Strecke [ P Q ] bestimmen:
Schritt einblenden / ausblenden
M → = 1 2 [ P → + Q → ] = 1 2 [ ( 2 2 3 ) + ( 0 0 1 ) ] = 1 2 ( 2 2 4 ) = ( 1 1 2 )

M ( 1 | 1 | 2 )
Symmetrieebene



E : x 1 + x 2 + x 3 = 4 ⇒ n E → = ( 1 1 1 )

P Q → = Q → - P → = ( 0 0 1 ) - ( 2 2 3 ) = ( - 2 - 2 - 2 ) = - 2 ⋅ ( 1 1 1 ) ︸ n E →
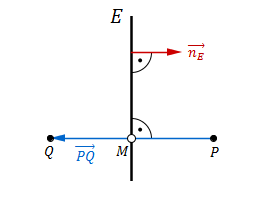
Der Vektor P Q → ist parallel zum Normalenvektor n E → der Ebene E , also steht er senkrecht zur Ebene E .
Schritt einblenden / ausblenden
Da zusätzlich M auf der Ebene E liegt ( 1 + 1 + 2 = 4 ), sind P und Q bezüglich der Ebene E symmetrisch.

Themen dieser Aufgabe:
Themen-Übersicht
Themen
Tipp:
Arbeite frühzeitig mit der Merkhilfe Mathematik,
die als Hilfsmittel im Abitur zugelassen ist.
Feedback:
Du hast einen Fehler gefunden oder hast Anregungen zur Internetseite?