Lösung Abitur Bayern 2014 Mathematik Analytische Geometrie V

zur Angabe dieser Abituraufgabe

Teilaufgabe Teil B e (4 BE)

Zeigen Sie, dass die Größe des Winkels

β

zwischen reflektiertem Lichtstrahl und Einfallslot mit der Größe des Winkels

α

zwischen einfallendem Lichtstrahl und Einfallslot übereinstimmt.

Lösung zu Teilaufgabe Teil B e

Winkel zwischen zwei Vektoren

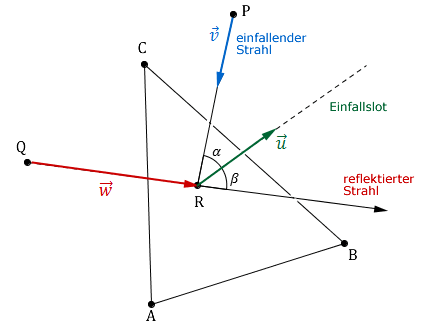
weitere Abituraufgaben zu diesem Thema

Richtungsvektor des einfallenden Strahls:

\vec{v} = (\begin{matrix} - 1 \\ - 1 \\ - 4 \end{matrix})

(s. Teil B Teilaufgabe b)

Richtungsvektor des reflektierten Strahls:

\vec{w} = (\begin{matrix} 1, 5 \\ 1, 5 \\ 0 \end{matrix})

(s. Teil B Teilaufgabe d)

Richtungsvektor des Einfallslot

\vec{u} = (\begin{matrix} 1 \\ 1 \\ 1 \end{matrix})

(s. Teil B Teilaufgabe d)

Winkel

α

und

β

bestimmen:

Schritt einblenden / ausblenden

Skalarprodukt

Winkel zwischen zwei Vektoren

Aus der allgemeinen Definition des Skalarproduktes zweier Vektoren

\vec{a}

und

\vec{b}

\vec{a} \circ \vec{b} = | \vec{a} | \cdot | \vec{b} | \cdot \cos \underset{α}{\underset{︸}{∡ (\vec{a}, \vec{b})}}

folgt für den Winkel

α

zwischen den beiden Vektoren:

\cos α = \frac{\vec{a} \circ \vec{b}}{| \vec{a} | \cdot | \vec{b} |}

(Formel zur Winkelberechnung zwischen 2 Vektoren)

\cos α = \frac{| \vec{v} \circ \vec{u} |}{| \vec{v} | \cdot | \vec{u} |}

;

\cos β = \frac{| \vec{w} \circ \vec{u} |}{| \vec{w} | \cdot | \vec{u} |}

\cos α = \frac{| (\begin{matrix} - 1 \\ - 1 \\ - 4 \end{matrix}) \circ (\begin{matrix} 1 \\ 1 \\ 1 \end{matrix}) |}{| (\begin{matrix} - 1 \\ - 1 \\ - 4 \end{matrix}) | \cdot | (\begin{matrix} 1 \\ 1 \\ 1 \end{matrix}) |}

;

\cos β = \frac{| (\begin{matrix} 1, 5 \\ 1, 5 \\ 0 \end{matrix}) \circ (\begin{matrix} 1 \\ 1 \\ 1 \end{matrix}) |}{| (\begin{matrix} 1, 5 \\ 1, 5 \\ 0 \end{matrix}) | \cdot | (\begin{matrix} 1 \\ 1 \\ 1 \end{matrix}) |}

Schritt einblenden / ausblenden

Die Länge (bzw. der Betrag)

| \vec{a} |

eines Vektors

\vec{a} = (\begin{matrix} a_{1} \\ a_{2} \\ a_{3} \end{matrix})

ist gegeben durch:

| \vec{a} | = | (\begin{matrix} a_{1} \\ a_{2} \\ a_{3} \end{matrix}) | = \sqrt{{(\begin{matrix} a_{1} \\ a_{2} \\ a_{3} \end{matrix})}^{2}} = \sqrt{a_{1}^{2} + a_{2}^{2} + a_{3}^{2}}

Hier:

| \vec{v} | = \sqrt{(- 1)^{2} + (- 1)^{2} + (- 4)^{2}} = \sqrt{18}

| \vec{u} | = \sqrt{1^{2} + 1^{2} + 1^{2}} = \sqrt{3}

| \vec{w} | = \sqrt{(1, 5)^{2} + (1, 5)^{2} + 0} = \sqrt{4, 5}

\cos α = \frac{6}{\sqrt{18} \cdot \sqrt{3}}

;

\cos β = \frac{3}{\sqrt{4, 5} \cdot \sqrt{3}}

\cos^{- 1} (\frac{6}{\sqrt{18} \cdot \sqrt{3}}) = \cos^{- 1} (\frac{3}{\sqrt{4, 5} \cdot \sqrt{3}}) \approx 35, 26^{\circ}

Alternative Lösung

weitere Abituraufgaben zu diesem Thema

Variante 1

Zeige durch Umformung, dass

\cos α = \cos β

Schritt einblenden / ausblenden

Umformung

\sqrt{18} = \sqrt{3^{2} \cdot 2} = \sqrt{3^{2}} \cdot \sqrt{2} = 3 \sqrt{2}

\sqrt{2} \cdot \sqrt{3} = \sqrt{2 \cdot 3} = \sqrt{6}

\sqrt{\frac{9}{2}} = \frac{\sqrt{9}}{\sqrt{2}} = \frac{3}{\sqrt{2}} = \frac{3}{\sqrt{2}} \cdot \frac{\sqrt{2}}{\sqrt{2}} = \frac{3 \sqrt{2}}{2}

\cos α = \frac{6}{\sqrt{18} \cdot \sqrt{3}} = \frac{6}{3 \sqrt{2} \cdot \sqrt{3}} = \frac{2}{\sqrt{6}}

\cos β = \frac{3}{\sqrt{4, 5} \cdot \sqrt{3}} = \frac{3}{\sqrt{\frac{9}{2}} \cdot \sqrt{3}} = \frac{3}{\frac{3}{\sqrt{2}} \cdot \sqrt{3}} = \frac{3}{\frac{3 \sqrt{2}}{2} \cdot \sqrt{3}} = \frac{2}{\sqrt{6}}

Aus

\cos α = \cos β

folgt

α = β

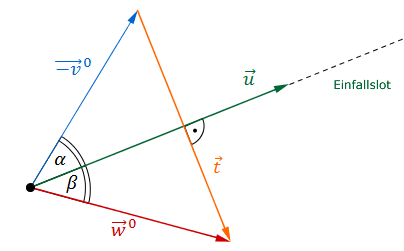
Variante 2

Einheitsvektoren

{\vec{w}}^{0}

und

{\vec{- v}}^{0}

bestimmen:

{\vec{w}}^{0} = \frac{1}{| \vec{w} |} \cdot \vec{w} = \frac{1}{\sqrt{4, 5}} (\begin{matrix} 1, 5 \\ 1, 5 \\ 0 \end{matrix}) = \frac{1}{\sqrt{18}} (\begin{matrix} 3 \\ 3 \\ 0 \end{matrix})

{\vec{- v}}^{0} = \frac{1}{| \vec{- v} |} \cdot \vec{v} = \frac{1}{\sqrt{18}} (\begin{matrix} 1 \\ 1 \\ 4 \end{matrix})

Verbindungsvektor

\vec{t}

zwischen

{\vec{w}}^{0}

und

{\vec{- v}}^{0}

bestimmen:

\vec{t} = {\vec{- v}}^{0} - {\vec{w}}^{0} = \frac{1}{\sqrt{18}} (\begin{matrix} 1 - 3 \\ 1 - 3 \\ 4 - 0 \end{matrix}) = \frac{1}{\sqrt{18}} (\begin{matrix} - 2 \\ - 2 \\ 4 \end{matrix})

Skalarprodukt mit

\vec{u}

bilden:

\frac{1}{\sqrt{18}} (\begin{matrix} - 2 \\ - 2 \\ 4 \end{matrix}) \circ (\begin{matrix} 1 \\ 1 \\ 1 \end{matrix}) = 0

\Rightarrow

\vec{t} ⊥ \vec{u}

Der Verbindungsvektor

\vec{t}

steht senkrecht auf den Richtungsvektor des Einfalllotes. Somit sind die Winkel gleichgroß.

Alle Abituraufgaben

Lösungen zu:

Teilaufgabe Teil A 1a

Teilaufgabe Teil A 1b

Teilaufgabe Teil A 2a

Teilaufgabe Teil A 2b

Teilaufgabe Teil B a

Teilaufgabe Teil B b

Teilaufgabe Teil B c

Teilaufgabe Teil B d

Teilaufgabe Teil B e

Lösung als Video:

Lösung als Video

Themen dieser Aufgabe:

Winkel zwischen zwei Vektoren

Alternative Lösung

Themen-Übersicht

Tipp:

Arbeite frühzeitig mit der Merkhilfe Mathematik,
die als Hilfsmittel im Abitur zugelassen ist.

Feedback:

Du hast einen Fehler gefunden oder hast Anregungen zur Internetseite?

Teile uns Dein Feedback mit!