über 250 kostenlose
Abituraufgaben
Lösung als Video
und ausformuliert
Alle Lösungen von
erfahrenen Lehrern
 
 
 
 
Lösung Abitur Bayern 2014 Mathematik Analytische Geometrie V


 
Teilaufgabe Teil B b  (5 BE)
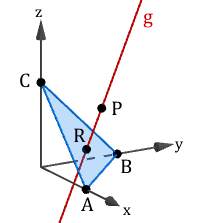
Das Dreieck A B C stellt modellhaft einen Spiegel dar. Der Punkt P ( 2 | 2 | 3 ) gibt im Modell die Position einer Lichtquelle an, von der ein Lichtstrahl ausgeht. Die Richtung dieses Lichtstrahls wird im Modell durch den Vektor v → = ( - 1 - 1 - 4 ) beschrieben.
Geben Sie eine Gleichung der Geraden g an, entlang derer der Lichtstrahl im Modell verläuft. Bestimmen Sie die Koordinaten des Punkts R , in dem g die Ebene E schneidet, und begründen Sie, dass der Lichtstrahl auf dem dreieckigen Spiegel auftrifft.

( zur Kontrolle: R ( 1 , 5 | 1 , 5 | 1 ) )

 
Lösung zu Teilaufgabe Teil B b

Geradengleichung aufstellen



g : X → = ( 2 2 3 ) ︸ P → + λ ⋅ ( - 1 - 1 - 4 ) ︸ v →
Schritt einblenden / ausblenden
Schnitt Ebene und Gerade



E : x 1 + x 2 + x 3 = 4

Ebene E und Gerade g schneiden: E ∩ g
Schritt einblenden / ausblenden
E ∩ g : ( 2 - λ ) + ( 2 - λ ) + ( 3 - 4 λ ) = 4 7 - 6 λ = 4 - 6 λ = - 3 λ = 1 2
Schritt einblenden / ausblenden
R → = ( 2 2 3 ) + 1 2 ⋅ ( - 1 - 1 - 4 ) = ( 1 , 5 1 , 5 1 ) ⇒ R ( 1 , 5 | 1 , 5 | 1 )



Begründung:
Schritt einblenden / ausblenden
Alle Koordinaten von R sind positiv.

Themen-Übersicht
Themen
Tipp:
Arbeite frühzeitig mit der Merkhilfe Mathematik,
die als Hilfsmittel im Abitur zugelassen ist.
Feedback:
Du hast einen Fehler gefunden oder hast Anregungen zur Internetseite?