über 250 kostenlose
Abituraufgaben
Lösung als Video
und ausformuliert
Alle Lösungen von
erfahrenen Lehrern
Abitur 2019 Mathematik Infinitesimalrechnung II
Gegeben ist die Funktion mit maximaler Definitionsmenge .
Teilaufgabe Teil A 1a (1 BE)
Geben Sie an.
Teilaufgabe Teil A 1b (4 BE)
Bestimmen Sie die Gleichung der Tangente an den Graphen von im Punkt .
| Gegeben ist die in definierte Funktion , die die Nullstellen und hat. Abbildung 1 zeigt den Graphen von , der symmetrisch bezüglich der y-Achse ist. Weiterhin ist die Gerade mit der Gleichung gegeben. | 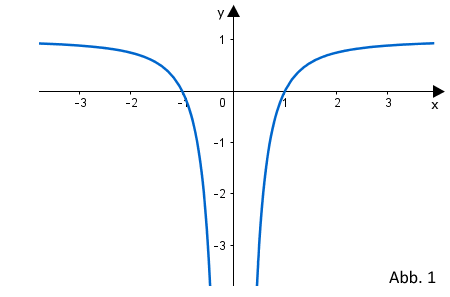 |
Teilaufgabe Teil A 2a (1 BE)
Zeigen Sie, dass einer der Punkte, in denen den Graphen von schneidet, die x-Koordinate hat.
Teilaufgabe Teil A 2b (4 BE)
Bestimmen Sie rechnerisch den Inhalt der Fläche, die der Graph von , die x-Achse und die Gerade einschließen.
Gegeben ist die Schar der in definierten Funktionen mit , deren Graphen Parabeln sind.
Teilaufgabe Teil A 3a (2 BE)
Bestimmen Sie den Wert von so, dass der Punkt auf der zugehörigen Parabel liegt.
Teilaufgabe Teil A 3b (3 BE)
Ermitteln Sie diejenigen Werte von , für die die jeweils zugehörige Funktion keine Nullstelle besitzt.
| Die nebenstehende Abbildung 2 zeigt den Graphen einer Funktion . | 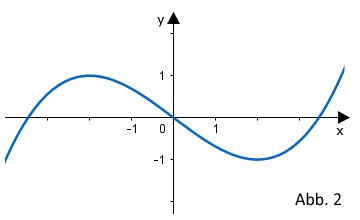 |
Teilaufgabe Teil A 4a (3 BE)
Einer der folgenden Graphen I, II und III gehört zur ersten Ableitungsfunktion von . Geben Sie diesen Graphen an. Begründen Sie, dass die beiden anderen Graphen dafür nicht infrage kommen.
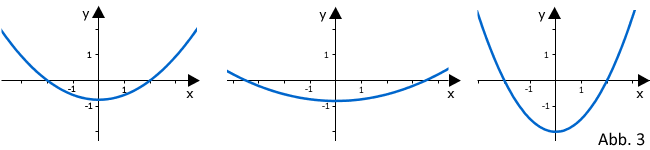

Teilaufgabe Teil A 4b (2 BE)
Die Funktion ist eine Stammfunktion von . Geben Sie das Monotonieverhalten von im Intervall an. Begründen Sie Ihre Angabe.
Gegeben ist die Funktion mit Definitionsmenge . Die Abbildung zeigt den Verlauf des Graphen von im I. Quadranten.
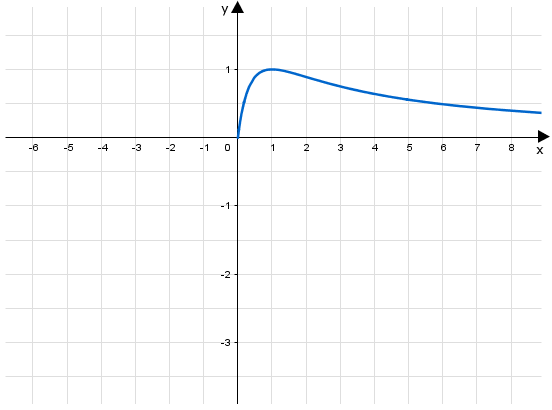
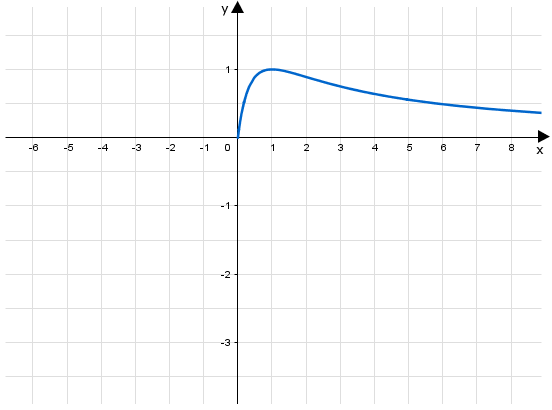
Teilaufgabe Teil B a (3 BE)
Begründen Sie, dass die einzige Nullstelle von ist. Geben Sie die Gleichung der senkrechten Asymptote von an und begründen Sie anhand des Funktionsterms von , dass die Gerade mit der Gleichung als waagrechte Asymptote besitzt.
Teilaufgabe Teil B b (5 BE)
Bestimmen Sie rechnerisch Lage und Art des Extrempunkts von .
Teilaufgabe Teil B c (4 BE)
Begründen Sie, dass für nur im III. Quadranten verläuft, und zeichnen Sie in die Abbildung den darin fehlenden Teil von ein. Berechnen Sie dazu und drei weitere geeignete Funktionswerte von .
Teilaufgabe Teil B d (3 BE)
Gegeben ferner die in definierte Funktion .
Zeigen Sie, dass für eine Stammfunktion von ist.
Zeigen Sie, dass für eine Stammfunktion von ist.
Ein Pharmaunternehmen führt eine Studie zur Wirksamkeit und Verträglichkeit eines neu entwickelten Medikaments durch. Wenn das Medikament einmalig in Form einer Tablette eingenommen wird, kann die zeitliche Entwicklung der Konzentration des Wirkstoffs im Blut des Patienten modellhaft durch die betrachtete Funktion für beschrieben werden. Dabei steht für die Zeit in Stunden seit der Einnahme der Tablette und für die Konzentration des Wirkstoffs im Blut des Patienten (im Weiteren kurz als Wirkstoffkonzentration bezeichnet) in Milligramm pro Liter .
Die folgenden Aufgaben e bis i sollen auf der Grundlage dieses Modells bearbeitet werden.
Die folgenden Aufgaben e bis i sollen auf der Grundlage dieses Modells bearbeitet werden.
Teilaufgabe Teil B e (2 BE)
Berechnen Sie die Wirkstoffkonzentration 30 Minuten nach Einnahme der Tablette und geben Sie die maximal auftretende Wirkstoffkonzentration an.
Teilaufgabe Teil B f (3 BE)
An der Stelle hat einen Wendepunkt. Beschreiben Sie, wie man rechnerisch vorgehen könnte, um dies zu begründen. Geben Sie die Bedeutung der x-Koordinate des Wendepunkts im Sachzusammenhang an.
In der Pharmakologie wird das in positive x-Richtung unbegrenzte Flächenstück, das sich im I. Quadranten zwischen und der x-Achse befindet, als AUC ("area under the curve") bezeichnet. Nur dann, wenn diesem Flächenstück ein endlicher Flächeninhalt zugeordnet werden kann, kann die betrachtete Funktion die zeitliche Entwicklung der Wirkstoffkonzentration auch für große Zeitwerte x realistisch beschreiben.
Teilaufgabe Teil B g (4 BE)
Die x-Achse, und die Gerade mit der Gleichung mit schließen im I. Quadranten ein Flächenstück mit dem Inhalt ein. Bestimmen Sie mithilfe der in Aufgabe d angegebenen Stammfunktion einen Term für und beurteilen Sie unter Verwendung dieses Terms, ob die Funktion auch für große Zeitwerte eine realistische Modellierung der zeitlichen Entwicklung der Wirkstoffkonzentration darstellt.
Das Medikament zeigt die gewünschte Wirkung erst ab einer bestimmten Wirkstoffkonzentration. Daher soll der Patient nach der ersten Tablette des Medikaments eine zweite identisch wirkende Tablette einnehmen, noch bevor die Konzentration des Wirkstoffs im Blut unter fällt. Nach der Einnahme der zweiten Tablette erhöht sich die Wirkstoffkonzentration um die durch diese Tablette verursachte Konzentration des Wirkstoffs im Blut.
Teilaufgabe Teil B h (4 BE)
Ermitteln Sie durch Rechnung den spätesten Zeitpunkt, zu dem die zweite Tablette eingenommen werden soll.
Teilaufgabe Teil B i (3 BE)
Wird die zweite Tablette zweieinhalb Stunden nach der ersten Tablette eingenommen, so kann die Wirkstoffkonzentration für mit einem der folgenden Terme beschrieben werden. Wählen Sie den passenden Term aus und begründen Sie Ihre Wahl.
(A)
(B)
(C)
(D)
(A)
(B)
(C)
(D)
Verabreicht man das Medikament nicht in Form von Tabletten, sondern mittels einer Dauerinfusion, so wird der Wirkstoff langsam und kontinuierlich zugeführt. Die in definierte Funktion beschreibt für modellhaft die zeitliche Entwicklung der Wirkstoffkonzentration während einer Dauerinfusion. Dabei ist die seit Anlegen der Dauerinfusion vergangene Zeit in Stunden und die Wirkstoffkonzentration in .
Teilaufgabe Teil B j (4 BE)
Begründen Sie, dass der Graph von streng monoton steigend ist.
(zur Kontrolle: )
(zur Kontrolle: )
Teilaufgabe Teil B k (5 BE)
Bei Dauerinfusionen dieses Medikaments muss die Wirkstoffkonzentration spätestens 60 Minuten nach Beginn der Infusion dauerhaft größer als sein und stets mindestens unter der gesundheitsschädlichen Grenze von liegen. Ermitteln Sie und beurteilen Sie beispielsweise unter Verwendung der bisherigen Ergebnisse, ob gemäß der Modellierung diese beiden Bedingungen erfüllt sind.
Lösungen zu:
Tipp:
Arbeite frühzeitig mit der Merkhilfe Mathematik,
die als Hilfsmittel im Abitur zugelassen ist.
die als Hilfsmittel im Abitur zugelassen ist.
Feedback:
Du hast einen Fehler gefunden oder hast Anregungen zur Internetseite?








