über 250 kostenlose
Abituraufgaben
Lösung als Video
und ausformuliert
Alle Lösungen von
erfahrenen Lehrern
Abitur 2017 Mathematik Infinitesimalrechnung I
Gegeben ist die Funktion mit maximaler Definitionsmenge . Der Graph von wird mit bezeichnet.
Teilaufgabe Teil A 1a (2 BE)
Geben Sie und die Koordinaten des Schnittpunkts von mit der y-Achse an.
Teilaufgabe Teil A 1b (4 BE)
Beschreiben Sie, wie schrittweise aus dem Graphen der in definierten Funktion hervorgeht, und geben Sie die Wertemenge von an.
Eine Funktion ist durch mit gegeben.
Teilaufgabe Teil A 2a (2 BE)
Ermitteln Sie die Nullstelle der Funktion .
Teilaufgabe Teil A 2b (3 BE)
Die Tangente an den Graphen von im Punkt begrenzt mit den beiden Koordinatenachsen ein Dreieck. Weisen Sie nach, dass dieses Dreieck gleichschenklig ist.
Geben Sie jeweils den Term einer Funktion an, die über ihrer maximalen Definitionsmenge die angegebenen Eigenschaften besitzt.
Teilaufgabe Teil A 3a (2 BE)
Der Graph der Funktion ist achsensymmetrisch zur y-Achse und die Gerade mit der Gleichung ist eine senkrechte Asymptote.
Teilaufgabe Teil A 3b (2 BE)
Die Funktion ist nicht konstant und es gilt .
An einer Messstation wurde über einen Zeitraum von 10 Stunden die Anzahl der Pollen in einem Kubikmeter Luft ermittelt. Dabei kann die Anzahl der Pollen in einem Kubikmeter Luft zum Zeitpunkt (in Stunden nach Beginn der Messung) durch die Gleichung beschrieben werden.
Teilaufgabe Teil A 4a (3 BE)
Bestimmen Sie die mittlere Änderungsrate der Anzahl der Pollen in einem Kubikmeter Luft während der ersten beiden Stunden der Messung.
Teilaufgabe Teil A 4b (2 BE)
Ermitteln Sie den Zeitpunkt nach Beginn der Messung, zu dem die momentane Änderungsrate der Anzahl der Pollen in einem Kubikmeter Luft beträgt.
Gegeben ist die in definierte Funktion .
Abbildung 1 zeigt den Graphen von im Bereich .
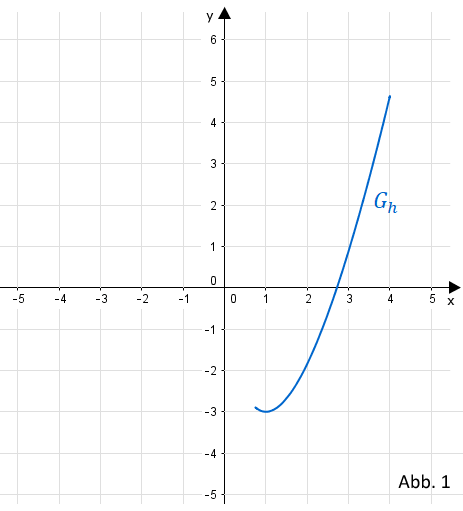
Abbildung 1 zeigt den Graphen von im Bereich .

Teilaufgabe Teil B 1a (4 BE)
Bestimmen Sie die Gleichung der Tangente an im Punkt und berechnen Sie die Größe des Winkels, unter dem diese Tangente die x-Achse schneidet.
(zur Kontrolle: )
Teilaufgabe Teil B 1b (4 BE)
Untersuchen Sie das Monotonieverhalten von . Geben Sie den Grenzwert von für an und begründen Sie, dass die Wertemenge von ist.
Teilaufgabe Teil B 1c (3 BE)
Geben Sie für die Funktion und deren Ableitungsfunktion jeweils das Verhalten für an und zeichnen Sie im Bereich in Abbildung 1 ein.
Die Funktion mit Definitionsmenge unterscheidet sich von der Funktion nur hinsichtlich der Definitionsmenge. Im Gegensatz zu ist die Funktion umkehrbar.
Teilaufgabe Teil B 1d (4 BE)
Geben Sie die Definitionsmenge und die Wertemenge der Umkehrfunktion von an. Berechnen Sie die Koordinaten des Schnittpunkts des Graphen von und der Geraden mit der Gleichung .
(Teilergebnis: x-Koordinate des Schnittpunkts: )
Teilaufgabe Teil B 1e (3 BE)
Zeichnen Sie den Graphen der Umkehrfunktion von unter Verwendung der bisherigen Ergebnisse, insbesondere der Lage von Punkt , in Abbildung 1 ein.
Teilaufgabe Teil B 1f (4 BE)
Schraffieren Sie in Abbildung 1 ein Flächenstück, dessen Inhalt dem Wert des Integrals entspricht, wobei die x-Koordinate von Punkt ist. Der Graph von , der Graph der Umkehrfunktion von sowie die beiden Koordinatenachsen schließen im ersten Quadranten ein Flächenstück mit Inhalt ein. Geben Sie unter Verwendung von einen Term zur Berechnung von an.
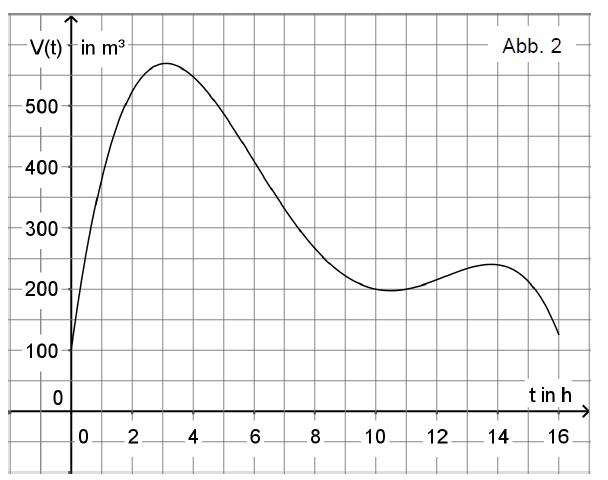
Abbildung 2 zeigt den Graphen einer in definierten Funktion . Sie beschreibt modellhaft das sich durch Zu- und Abfluss ändernde Volumen von Wasser in einem Becken in Abhängigkeit von der Zeit. Dabei bezeichnen die seit Beobachtungsbeginn vergangene Zeit in Stunden und das Volumen in Kubikmetern.

Teilaufgabe Teil B 2a (2 BE)
Geben Sie mithilfe von Abbildung 2 jeweils näherungsweise das Volumen des Wassers fünf Stunden nach Beobachtungsbeginn sowie den Zeitraum an, in dem das Volumen mindestens beträgt.
Teilaufgabe Teil B 2b (3 BE)
Bestimmen Sie anhand des Graphen der Funktion näherungsweise die momentane Änderungsrate des Wasservolumens zwei Stunden nach Beobachtungsbeginn.
Teilaufgabe Teil B 2c (3 BE)
Erläutern Sie, was es im Sachzusammenhang bedeutet, wenn für ein die Beziehung gilt. Entscheiden Sie mithilfe von Abbildung 2, ob für diese Beziehung gilt, und begründen Sie Ihre Entscheidung.
In einem anderen Becken ändert sich das Volumen des darin enthaltenen Wassers ebenfalls durch Zu- und Abfluss. Die momentane Änderungsrate des Volumens wird für modellhaft durch die in definierte Funktion beschrieben. Dabei ist die seit Beobachtungsbeginn vergangene Zeit in Stunden und die momentane Änderungsrate des Volumens in .
Teilaufgabe Teil B 2d (4 BE)
Begründen Sie, dass die Funktionswerte von für positiv und für negativ sind.
Teilaufgabe Teil B 2e (6 BE)
Erläutern Sie die Bedeutung des Werts des Integrals für im Sachzusammenhang. Berechnen Sie das Volumen des Wassers, das sich 7,5 Stunden nach Beobachtungsbeginn im Becken befindet, wenn zu Beobachtungsbeginn Wasser im Becken waren. Begründen Sie, dass es sich hierbei um das maximale Wasservolumen im Beobachtungszeitraum handelt.
Lösungen zu:
Tipp:
Arbeite frühzeitig mit der Merkhilfe Mathematik,
die als Hilfsmittel im Abitur zugelassen ist.
die als Hilfsmittel im Abitur zugelassen ist.
Feedback:
Du hast einen Fehler gefunden oder hast Anregungen zur Internetseite?








