über 250 kostenlose
Abituraufgaben
Lösung als Video
und ausformuliert
Alle Lösungen von
erfahrenen Lehrern
Lösung Abitur Bayern 2010 Mathematik LK Infinitesimalrechnung II
Teilaufgabe 2c (5 BE)
Begründen Sie, dass für gilt: .
Welche Bedeutung hat diese Beziehung für den Graphen der Integralfunktion ?
Welche Bedeutung hat diese Beziehung für den Graphen der Integralfunktion ?
Lösung zu Teilaufgabe 2c
Eigenschaften der Integralfunktion
Begründung:
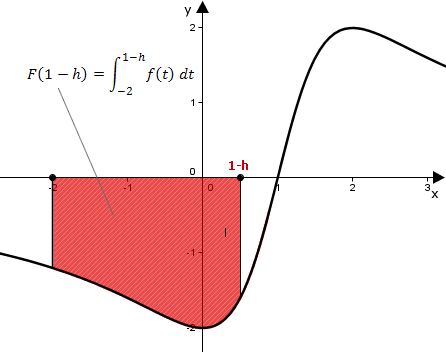
entspricht der Fläche die der Graph mit der -Achse zwischen und einschließt.
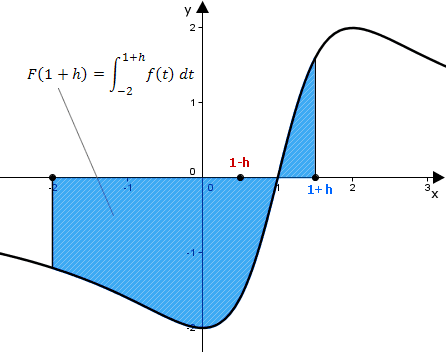
entspricht der Fläche die der Graph mit der -Achse zwischen und einschließt.
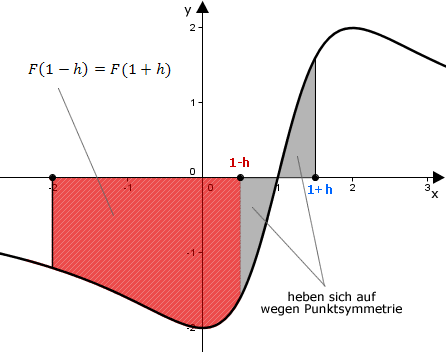
Wegen der Punktsymmetrie der Funktion zum Punkt , ist die Fläche die der Graph mit der -Achse zwischen und einschließt betragsmäßig gleichgroß wie die Fläche zwischen und . Somit heben sich diese Flächen bei der Berechnung von gegenseitig auf (da verschiedenes Vorzeichen).
für
Der Graph der Integralfunktion ist achsensymmetrisch bezüglich
für
Der Graph der Integralfunktion ist achsensymmetrisch bezüglich
Alternative Lösung
Lösungen zu:
Themen dieser Aufgabe:
Tipp:
Arbeite frühzeitig mit der Merkhilfe Mathematik,
die als Hilfsmittel im Abitur zugelassen ist.
die als Hilfsmittel im Abitur zugelassen ist.
Feedback:
Du hast einen Fehler gefunden oder hast Anregungen zur Internetseite?








