über 250 kostenlose
Abituraufgaben
Lösung als Video
und ausformuliert
Alle Lösungen von
erfahrenen Lehrern
 
 
 
 
AB SOFORT: KEIN LOGIN mehr erforderlich - alle Lösungen zu den Abituraufgaben sind frei zugänglich.
 

Abitur 2010 Mathematik LK Infinitesimalrechnung II

Gegeben ist die Schar der Funktionen g k : x ↦ x 2 - k x 2 - 1 mit k ∈ ℝ + ∖ { 1 } und Definitionsmenge D = ℝ ∖ { - 1 ; 1 } . Der Graph von g k wird mit G k
bezeichnet.
Teilaufgabe 1a  (6 BE)

Untersuchen Sie G k auf Symmetrie, bestimmen Sie die Schnittpunkte von G k mit den Koordinatenachsen und geben Sie die Gleichungen aller Asymptoten an.

Teilaufgabe 1b  (6 BE)

Zeigen Sie, dass G k genau einen Extrempunkt besitzt, und bestimmen Sie dessen Lage und Art in Abhängigkeit von k .

Teilaufgabe 1c  (6 BE)

Wählen Sie zwei Scharparameter k 1 und k 2 so, dass sich die zugehörigen Graphen in der Art ihres Extrempunkts unterscheiden. Skizzieren Sie G k 1 und G k 2 unter Verwendung der bisherigen Ergebnisse in ein geeignetes Koordinatensystem.

Die Abbildung zeigt den Graphen G f einer in ℝ definierten, stetigen Funktion f . G f ist punktsymmetrisch zum einzigen Schnittpunkt S ( 1 | 0 ) mit der x -Achse. Die Extrempunkte von G f sind ( 0 | - 2 ) und ( 2 | 2 ) .
Die Funktion F : x ↦ ∫ - 2 x f ( t ) d t mit x ∈ ℝ ist eine Integralfunktion von f .

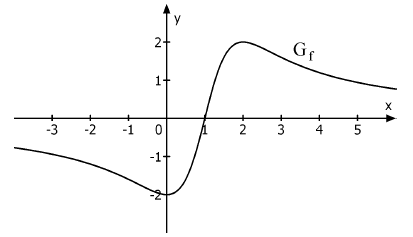
Teilaufgabe 2a  (5 BE)

Geben Sie Monotonie- und Krümmungsverhalten des Graphen von F an.

Teilaufgabe 2b  (4 BE)

Begründen Sie, dass F genau zwei Nullstellen hat, und geben Sie diese an.

Teilaufgabe 2c  (5 BE)

Begründen Sie, dass für h > 0 gilt: F ( 1 - h ) = F ( 1 + h ) .
Welche Bedeutung hat diese Beziehung für den Graphen der Integralfunktion F ?

Für die Abschätzung des Risikos von Meteoriteneinschlägen auf der Erde spielt die folgende Funktionenschar eine zentrale Rolle:
φ λ : t ↦ λ e - λ t , t ≠ 0 , λ > 0
t gibt die Wartezeit bis zum ersten Einschlag in Jahren an. λ ist ein von der Meteoritengröße abhängiger Parameter.
Für einen Zeitpunkt t 1 > 0 entspricht der Inhalt der schraffierten Fläche (vgl. Skizze) der Wahrscheinlichkeit, dass bis zum Zeitpunkt t 1 der erste Meteoriteneinschlag erfolgt ist.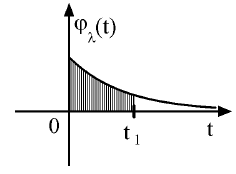
Teilaufgabe 3a  (3 BE)

Berechnen Sie die Wahrscheinlichkeit dafür, dass bis zum Zeitpunkt t 1 = 1 λ der erste Einschlag erfolgt ist.

Teilaufgabe 3b  (5 BE)

Berechnen Sie die mittlere Wartezeit T ¯ (in Jahren) bis zum ersten Einschlag, die durch T ¯ = ∫ 0 ∞ t ⋅ φ λ ( t ) d t gegeben ist.

Lösung als Video:

 
Themen-Übersicht
Themen
Tipp:
Arbeite frühzeitig mit der Merkhilfe Mathematik,
die als Hilfsmittel im Abitur zugelassen ist.
Feedback:
Du hast einen Fehler gefunden oder hast Anregungen zur Internetseite?