über 250 kostenlose
Abituraufgaben
Lösung als Video
und ausformuliert
Alle Lösungen von
erfahrenen Lehrern

Lösung Abitur Bayern 2010 Mathematik GK Stochastik III

zur Angabe dieser Abituraufgabe
Teilaufgabe 5  (5 BE)
Von einer Bergstation führen zwei Abfahrten ins Tal, eine einfache "blaue" und eine anspruchsvolle "schwarze". Im Auftrag der ortsansässigen Skischule wird untersucht, ob die Wahl der Abfahrt geschlechtsabhängig ist. Eine über mehrere Wochen erstellte Statistik über die von der Bergstation abfahrenden Personen zeigt, dass 45 % unter ihnen weiblich sind; 22 % unter ihnen sind männlich und entscheiden sich für die schwarze Abfahrt, 27 % unter ihnen sind weiblich und wählen die blaue Abfahrt.
Eine in der Statistik erfasste Person wird zufällig ausgewählt. Untersuchen Sie die beiden Ereignisse "Die ausgewählte Person ist männlich" und "Die ausgewählte Person entscheidet sich für die blaue Abfahrt" auf stochastische Unabhängigkeit.
 
Lösung zu Teilaufgabe 5
Vierfeldertafel für zwei Ereignisse



Daten aus der Aufgabenstellung analysieren:

Ereignisse:

M : "Person ist männlich"
W : "Person ist weiblich"

B : "Blaue Abfahrt"
S : "Schwarze Abfahrt"


Wahrscheinlichkeiten:

45 % sind weiblich
⇒ P ( W ) = 0 , 45

22 % sind männlich und entscheiden sich für die schwarze Piste
⇒ P ( M ∩ S ) = 0 , 22

27 % sind weiblich und entscheiden sich für die blaue Piste
⇒ P ( W ∩ B ) = 0 , 27
Vier-Felder-Tafel aus obigen Daten erstellen:
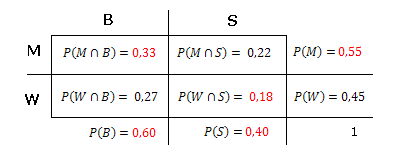
Stochastische Unabhängigkeit



Überprüfen ob gilt: P ( M ∩ B ) = P ( M ) ⋅ P ( B )
Schritt einblenden / ausblenden
P ( M ∩ B ) = ! P ( M ) ⋅ P ( B )

0 , 33 = 0 , 55 ⋅ 0 , 60 ︸ 0 , 33


⇒ Die Ereignisse M und B sind stochastisch unabhängig!
Alle Abituraufgaben
Lösungen zu:
Teilaufgabe 1
Teilaufgabe 2a
Teilaufgabe 2b
Teilaufgabe 3a
Teilaufgabe 3b
Teilaufgabe 3c
Teilaufgabe 4
Teilaufgabe 5
Teilaufgabe 6a
Teilaufgabe 6b
Lösung als Video:
Lösung als Video
Themen dieser Aufgabe:
Vierfeldertafel für zwei Ereignisse
Stochastische Unabhängigkeit
Themen-Übersicht
Themen
Tipp:
Arbeite frühzeitig mit der Merkhilfe Mathematik,
die als Hilfsmittel im Abitur zugelassen ist.
Feedback:

Du hast einen Fehler gefunden oder hast Anregungen zur Internetseite?

Teile uns Dein Feedback mit!