Toggle navigation

Alle Abituraufgaben

Lösungen zu:

Teilaufgabe 1a

Teilaufgabe 1b

Teilaufgabe 1c

Teilaufgabe 2a

Teilaufgabe 2b

Teilaufgabe 2c

Teilaufgabe 2d

Teilaufgabe 3

Lösung als Video:

Themen dieser Aufgabe:

Lotfußpunkt auf eine Ebene

Schnitt Ebene und Gerade

Lage eines Punktes

Themen-Übersicht

Tipp:

Arbeite frühzeitig mit der Merkhilfe Mathematik,
die als Hilfsmittel im Abitur zugelassen ist.

Feedback:

Du hast einen Fehler gefunden oder hast Anregungen zur Internetseite?

Teile uns Dein Feedback mit!

Lösung Abitur Bayern 2008 Mathematik LK Analytische Geometrie V

zur Angabe dieser Abituraufgabe

Teilaufgabe 2c (7 BE)

Nun sei $t = 1$ . Die durch die Punkte $A, D$ und $S_{1}$ festgelegte
Seitenfläche des Parallelflachs liegt in der Ebene $F : 2 x_{1} - x_{3} + 1 = 0$ .

Im Punkt $T (1 | 5 | 3)$ dieser Seitenfläche wird ein Lot errichtet.
Berechnen Sie die Koordinaten des Punktes $U$ , in dem das Lot die Ebene $E$ schneidet, und zeigen Sie, dass $U$ nicht im Innern des Quadrats $A B C D$ liegt.

Lösung zu Teilaufgabe 2c

Lösung als Video

Lotfußpunkt auf eine Ebene

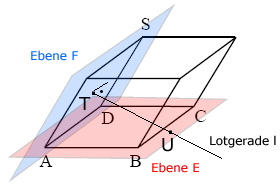
weitere Abituraufgaben zu diesem Thema

$F : 2 x_{1} - x_{3} + 1 = 0$

$\Rightarrow \vec{n_{F}} = (\begin{matrix} 2 \\ 0 \\ - 1 \end{matrix})$ Normalenvektor der Ebene $F$

$T (1 | 5 | 3)$

Gleichung der Lotgerade aufstellen:

Schritt einblenden / ausblenden

$l : \vec{x} = (\begin{matrix} 1 \\ 5 \\ 3 \end{matrix}) + σ \cdot (\begin{matrix} 2 \\ 0 \\ - 1 \end{matrix})$

Schnitt Ebene und Gerade

weitere Abituraufgaben zu diesem Thema

$E_{A B D} : \vec{x} \cdot (\begin{matrix} 2 \\ 2 \\ 1 \end{matrix}) = 9$ (siehe Teilaufgabe 1a)

Gesucht ist $l \cap E_{A B D}$ :

Schritt einblenden / ausblenden

$[(\begin{matrix} 1 \\ 5 \\ 3 \end{matrix}) + σ \cdot (\begin{matrix} 2 \\ 0 \\ - 1 \end{matrix})] \cdot (\begin{matrix} 2 \\ 2 \\ 1 \end{matrix}) = 9$

$\Rightarrow (1 + 2 σ) \cdot 2 + (5 + 0 \cdot σ) \cdot 2 + (3 - σ) \cdot 1 = 9$

$\Rightarrow 2 + 4 σ + 10 + 3 - σ = 9$

$\Rightarrow 3 σ = - 6$

$\Rightarrow σ = - 2$

$σ = - 2$ in die Geradengleichung einsetzen:

$\vec{O U} = (\begin{matrix} 1 \\ 5 \\ 3 \end{matrix}) - 2 \cdot (\begin{matrix} 2 \\ 0 \\ - 1 \end{matrix}) = (\begin{matrix} - 3 \\ 5 \\ 5 \end{matrix})$

Das Lot $l$ schneidet die Ebene $E_{A B D}$ im Punkt $U (- 3 | 5 | 5)$ .

Lage eines Punktes

weitere Abituraufgaben zu diesem Thema

Parameterform der Ebene $E_{A B D}$ (siehe Teilaufgabe 1a):

Schritt einblenden / ausblenden

$\vec{x} = (\begin{matrix} 1 \\ 2 \\ 3 \end{matrix}) + ρ \cdot (\begin{matrix} 4 \\ - 2 \\ - 4 \end{matrix}) + τ \cdot (\begin{matrix} - 2 \\ 4 \\ - 4 \end{matrix})$

Da $U \in E_{A B D}$ gilt:

$(\begin{matrix} - 3 \\ 5 \\ 5 \end{matrix}) = (\begin{matrix} 1 \\ 2 \\ 3 \end{matrix}) + ρ \cdot (\begin{matrix} 4 \\ - 2 \\ - 4 \end{matrix}) + τ \cdot (\begin{matrix} - 2 \\ 4 \\ - 4 \end{matrix})$

$α$ und $β$ bestimmen:

$\begin{matrix} (I) \\ (I I) \\ (I I I) \end{matrix}$ $\begin{matrix} - 3 & = & 1 + 4 ρ - 2 τ \\ 5 & = & 2 - 2 ρ + 4 τ \\ 5 & = & 3 - 4 ρ - 4 τ \end{matrix}$

Gleichung (I) durch 2 teilen

$\begin{matrix} (I) \\ (I I) \\ (I I I) \end{matrix}$ $\begin{matrix} - 2 & = & 2 ρ - τ \\ 3 & = & - 2 ρ + 4 τ \\ 2 & = & - 4 ρ - 4 τ \end{matrix}$

Gleichung (I) zur Gleichung (II) addieren

$1 = 3 τ \Rightarrow τ = \frac{1}{3}$

$τ$ in Gleichung (II) einsetzen:

$3 = - 2 ρ + 4 \cdot \frac{1}{3} \Rightarrow \frac{5}{3} = - 2 ρ \Rightarrow ρ = - \frac{5}{6}$

Schritt einblenden / ausblenden

$\Rightarrow$ Der Punkt $U$ liegt nicht im Inneren des Quadrates.

Alle Abituraufgaben

Lösungen zu:

Teilaufgabe 1a

Teilaufgabe 1b

Teilaufgabe 1c

Teilaufgabe 2a

Teilaufgabe 2b

Teilaufgabe 2c

Teilaufgabe 2d

Teilaufgabe 3

Lösung als Video:

Themen dieser Aufgabe:

Lotfußpunkt auf eine Ebene

Schnitt Ebene und Gerade

Lage eines Punktes

Themen-Übersicht

Tipp:

Arbeite frühzeitig mit der Merkhilfe Mathematik,
die als Hilfsmittel im Abitur zugelassen ist.

Feedback:

Du hast einen Fehler gefunden oder hast Anregungen zur Internetseite?

Teile uns Dein Feedback mit!