Toggle navigation

Alle Abituraufgaben

Lösungen zu:

Teilaufgabe 1a

Teilaufgabe 1b

Teilaufgabe 1c

Teilaufgabe 2a

Teilaufgabe 2b

Teilaufgabe 2c

Teilaufgabe 2d

Teilaufgabe 3

Lösung als Video:

Themen dieser Aufgabe:

Abstand Punkt - Ebene

Volumen eines Prismas

Themen-Übersicht

Tipp:

Arbeite frühzeitig mit der Merkhilfe Mathematik,
die als Hilfsmittel im Abitur zugelassen ist.

Feedback:

Du hast einen Fehler gefunden oder hast Anregungen zur Internetseite?

Teile uns Dein Feedback mit!

Lösung Abitur Bayern 2008 Mathematik LK Analytische Geometrie V

zur Angabe dieser Abituraufgabe

Teilaufgabe 2a (6 BE)

Das Quadrat $A B C D$ als Begrenzungsfläche und die Strecke $[D S_{t}]$ als Seitenkante bestimmen ein Parallelflach.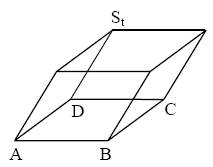

Berechnen Sie alle Werte von $t$ , für die das Parallelflach den Rauminhalt $V = 144$ hat.

Lösung zu Teilaufgabe 2a

Lösung als Video

Abstand Punkt - Ebene

weitere Abituraufgaben zu diesem Thema

$S_{t} (1 - t | 8 | t)$

$E_{A B C D} : \vec{x} \cdot (\begin{matrix} 2 \\ 2 \\ 1 \end{matrix}) - 9 = 0$ (siehe Teilaufgabe 1a)

Hesse-Normalenform der Ebene bilden:

Schritt einblenden / ausblenden

$E_{A B C D}^{H N F} : \frac{\vec{x} \cdot (\begin{matrix} 2 \\ 2 \\ 1 \end{matrix}) - 9}{| (\begin{matrix} 2 \\ 2 \\ 1 \end{matrix}) |} = 0$

$E_{A B C D}^{H N F} : \frac{\vec{x} \cdot (\begin{matrix} 2 \\ 2 \\ 1 \end{matrix}) - 9}{\sqrt{{(\begin{matrix} 2 \\ 2 \\ 1 \end{matrix})}^{2}}} = 0$

$E_{A B C D}^{H N F} : \frac{\vec{x} \cdot (\begin{matrix} 2 \\ 2 \\ 1 \end{matrix}) - 9}{\sqrt{2^{2} + 2^{2} + 1^{2}}} = 0$

$E_{A B C D}^{H N F} : \frac{\vec{x} \cdot (\begin{matrix} 2 \\ 2 \\ 1 \end{matrix}) - 9}{3} = 0$

Abstand des Punktes $S_{t}$ zur Ebene bestimmen:

Schritt einblenden / ausblenden

$d (S_{t}) = | E^{H N F} (S_{t}) |$

$= | \frac{(\begin{matrix} 1 - t \\ 8 \\ t \end{matrix}) \cdot (\begin{matrix} 2 \\ 2 \\ 1 \end{matrix}) - 9}{3} |$

$= | \frac{2 (1 - t) + 16 + t - 9}{3} |$

$= | \frac{9 - t}{3} |$

$= \frac{1}{3} | 9 - t |$

Die Höhe $h (t)$ ist also gleich:

Schritt einblenden / ausblenden

$h (t) = \frac{1}{3} | 9 - t |$

Volumen eines Prismas

weitere Abituraufgaben zu diesem Thema

Grundfläche des Parallelflachs ist das Quadrat $A B C D$ :

$G = {\bar{A B}}^{2} = 6^{2} = 36$ (siehe Teilaufgabe 1b)

Das Volumen des Parallelflachs ist dann gleich:

$V = 36 \cdot h (t) = 36 \cdot \frac{1}{3} | 9 - t | = 12 \cdot | 9 - t |$

Es soll gelten: $V = 144$

$\Rightarrow 12 \cdot | 9 - t | = 144$

$| 9 - t | = 12$

$\pm (9 - t) = 12$

$\Rightarrow t_{1} = - 3$ und $t_{2} = 21$

Alle Abituraufgaben

Lösungen zu:

Teilaufgabe 1a

Teilaufgabe 1b

Teilaufgabe 1c

Teilaufgabe 2a

Teilaufgabe 2b

Teilaufgabe 2c

Teilaufgabe 2d

Teilaufgabe 3

Lösung als Video:

Themen dieser Aufgabe:

Abstand Punkt - Ebene

Volumen eines Prismas

Themen-Übersicht

Tipp:

Arbeite frühzeitig mit der Merkhilfe Mathematik,
die als Hilfsmittel im Abitur zugelassen ist.

Feedback:

Du hast einen Fehler gefunden oder hast Anregungen zur Internetseite?

Teile uns Dein Feedback mit!