über 250 kostenlose
Abituraufgaben
Lösung als Video
und ausformuliert
Alle Lösungen von
erfahrenen Lehrern
Toggle navigation
Lösungen zu:
Lösung als Video:
Themen-Übersicht
Tipp:
Arbeite frühzeitig mit der Merkhilfe Mathematik,
die als Hilfsmittel im Abitur zugelassen ist.
Feedback:
Du hast einen
Fehler
gefunden oder hast Anregungen zur Internetseite?
Abitur 2008 Mathematik LK Analytische Geometrie V
Lösungen zu:
Lösung als Video:
Themen-Übersicht
Tipp:
Arbeite frühzeitig mit der Merkhilfe Mathematik,
die als Hilfsmittel im Abitur zugelassen ist.
die als Hilfsmittel im Abitur zugelassen ist.
Feedback:
Du hast einen Fehler gefunden oder hast Anregungen zur Internetseite?
Gegeben sind in einem kartesischen Koordinatensystem des die Punkte und sowie mit als Parameter.
Teilaufgabe 1a (5 BE)
Zeigen Sie, dass die Punkte und eine Ebene bestimmen, und ermitteln Sie eine Gleichung der Ebene in Normalenform.
[Zur Kontrolle: ]
[Zur Kontrolle: ]
Teilaufgabe 1b (4 BE)
Weisen Sie nach, dass sich die Punkte und durch einen vierten Punkt zu einem Quadrat ergänzen lassen, und berechnen Sie den Diagonalenschnittpunkt dieses Quadrats.
[Teilergebnis: ]
[Teilergebnis: ]
Teilaufgabe 1c (5 BE)
Für welchen Wert von ist die Entfernung von zu minimal?
| Das Quadrat als Begrenzungsfläche und die Strecke als Seitenkante bestimmen ein Parallelflach. |  |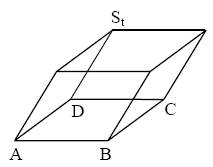
Teilaufgabe 2a (6 BE)
Berechnen Sie alle Werte von , für die das Parallelflach den Rauminhalt hat.
Teilaufgabe 2b (3 BE)
Bestimmen Sie so, dass das Parallelflach ein Quader ist.
Nun sei . Die durch die Punkte und festgelegte
Seitenfläche des Parallelflachs liegt in der Ebene .
Seitenfläche des Parallelflachs liegt in der Ebene .
Teilaufgabe 2c (7 BE)
Im Punkt dieser Seitenfläche wird ein Lot errichtet.
Berechnen Sie die Koordinaten des Punktes , in dem das Lot die Ebene schneidet, und zeigen Sie, dass nicht im Innern des Quadrats liegt.
Berechnen Sie die Koordinaten des Punktes , in dem das Lot die Ebene schneidet, und zeigen Sie, dass nicht im Innern des Quadrats liegt.
Teilaufgabe 2d (3 BE)
Ermitteln Sie den Schnittwinkel der Ebenen und .
Teilaufgabe 3 (7 BE)
sei die Kugel, die den Punkt aus Teilaufgabe 1b als Mittelpunkt und den Radius hat. Sie wird durch eine zentrische Streckung mit als Zentrum und dem Streckungsfaktor auf die Kugel abgebildet.
Ermitteln Sie die Koordinaten des Mittelpunkts von sowie den maximalen Abstand, den zwei Punkte und haben können, wenn auf und auf liegt.
Ermitteln Sie die Koordinaten des Mittelpunkts von sowie den maximalen Abstand, den zwei Punkte und haben können, wenn auf und auf liegt.
Lösungen zu:
Lösung als Video:
Themen-Übersicht
Tipp:
Arbeite frühzeitig mit der Merkhilfe Mathematik,
die als Hilfsmittel im Abitur zugelassen ist.
die als Hilfsmittel im Abitur zugelassen ist.
Feedback:
Du hast einen Fehler gefunden oder hast Anregungen zur Internetseite?
© 2001 - 2025 Abiturloesung.de. Alle Rechte vorbehalten.
