über 250 kostenlose
Abituraufgaben
Lösung als Video
und ausformuliert
Alle Lösungen von
erfahrenen Lehrern

Lösung Abitur Bayern 2021 Mathematik Analytische Geometrie V

zur Angabe dieser Abituraufgabe
Teilaufgabe Teil B a  (4 BE)
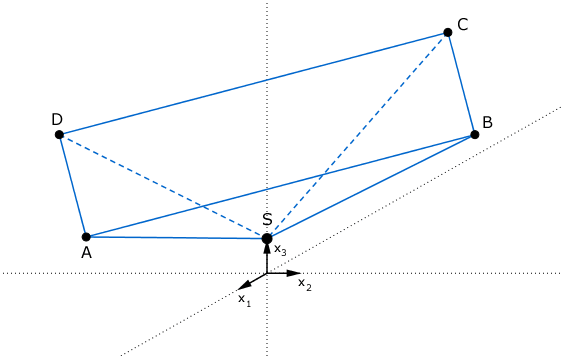
Die Punkte A ( 6 | 0 | 4 ) , B ( 0 | 6 | 4 ) , C ( - 6 | 0 | 4 ) und D liegen in der Ebene E und bilden die Eckpunkte der quadratischen Grundfläche einer Pyramide ABCDS mit der Spitze S ( 0 | 0 | 1 ) . A , B und S liegen in der Ebene F .
Zeigen Sie rechnerisch, dass das Dreieck ABS gleichschenklig ist. Geben Sie die Koordinaten des Punkts D an und beschreiben Sie die besondere Lage der Ebene E im Koordinatensystem.
 
Lösung zu Teilaufgabe Teil B a
Nachweis - gleichschenkliges Dreieck



SA → = A → - S → = ( 6 0 4 ) - ( 0 0 1 ) = ( 6 0 3 )

SB → = B → - S → = ( 0 6 4 ) - ( 0 0 1 ) = ( 0 6 3 )
Schritt einblenden / ausblenden
⇒ | SA → | = | SB → |
⇒ △ ABS ist gleichschenklig
Lage eines Punktes



D ( 0 | - 6 | 4 )
Schritt einblenden / ausblenden
Lagebeziehung von Ebenen



Die Ebene E ist parallel zur x 1 x 2 -Ebene.
Alle Abituraufgaben
Lösungen zu:
Teilaufgabe Teil A a
Teilaufgabe Teil A b
Teilaufgabe Teil B a
Teilaufgabe Teil B b
Teilaufgabe Teil B c
Teilaufgabe Teil B d
Teilaufgabe Teil B e
Teilaufgabe Teil B f
Teilaufgabe Teil B g
Teilaufgabe Teil B h
Lösung als Video:
Lösung als Video
Themen dieser Aufgabe:
Nachweis - gleichschenkliges Dreieck
Lage eines Punktes
Lagebeziehung von Ebenen
Themen-Übersicht
Themen
Tipp:
Arbeite frühzeitig mit der Merkhilfe Mathematik,
die als Hilfsmittel im Abitur zugelassen ist.
Feedback:

Du hast einen Fehler gefunden oder hast Anregungen zur Internetseite?

Teile uns Dein Feedback mit!