Lösung Abitur Bayern 2017 Mathematik Analytische Geometrie VI

zur Angabe dieser Abituraufgabe

Teilaufgabe Teil B d (4 BE)

Im Zelt ist eine Lichtquelle so aufgehängt, dass sie von jeder der vier Wände einen Abstand von

50 cm

hat. Ermitteln Sie die Koordinaten des Punkts, der im Modell die Lichtquelle darstellt.

Lösung zu Teilaufgabe Teil B d

Geradengleichung aufstellen

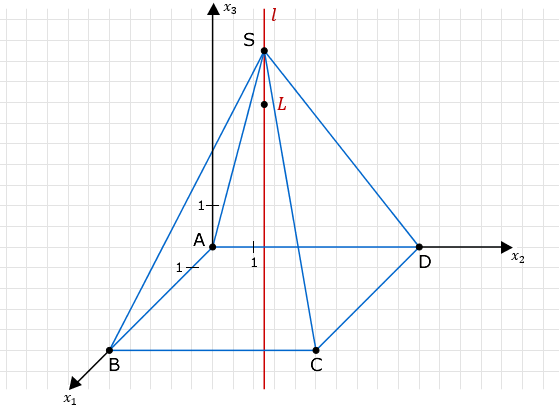
weitere Abituraufgaben zu diesem Thema

Schritt einblenden / ausblenden

Gerade Pyramide

Die Pyramide

A B C D S

ist eine gerade Pyramide, da alle Seitenkanten gleich lang sind (s. Teil B Teilaufgabe a) und die Spitze

S

senkrecht über den Diagonalenschnittpunkt der Grundfläche liegt (Grundfläche ist ein Quadrat mit Seitenlänge 5 und die

x_{1}

und

x_{2}

-Koordinate von

S

ist gleich 2,5).

Das Lot von

S

auf die Grundfläche verläuft somit durch den Diagonalenschnittpunkt der Grundfläche.

Die Lichtquelle befindest sich somit auf dieser Lotgeraden.

Gerade

l

durch

S

parallel zur

x_{3}

-Achse aufstellen:

Schritt einblenden / ausblenden

Geradengleichung

Eine Gerade

g

ist durch einen Ortsvektor

\vec{P}

und einen Richtungsvektor

\vec{v}

eindeutig bestimmt:

g : \vec{X} = \vec{P} + μ \cdot \vec{v}

μ \in ℝ

Wenn hier

S

als Aufpunkt genommen wird, dann ist

\vec{S}

der Ortsvektor (des Aufpunkts) der Geraden

l

l : \vec{X} = \underset{\vec{S}}{\underset{︸}{(\begin{matrix} 2, 5 \\ 2, 5 \\ 6 \end{matrix})}} + λ (\begin{matrix} 0 \\ 0 \\ 1 \end{matrix})

l : \vec{X} = (\begin{matrix} 2, 5 \\ 2, 5 \\ 6 + λ \end{matrix})

Abstand Punkt - Ebene

weitere Abituraufgaben zu diesem Thema

E : 12 x_{2} + 5 x_{3} - 60 = 0

\vec{n_{E}} = (\begin{matrix} 0 \\ 12 \\ 5 \end{matrix})

Normalenvektor der Ebene

| \vec{n_{E}} | = | (\begin{matrix} 0 \\ 12 \\ 5 \end{matrix}) | = \sqrt{0 + 12^{2} + 5^{2}} = \sqrt{169} = 13

Hesse-Normalenform

E^{HNF}

der Ebene aufstellen:

Schritt einblenden / ausblenden

Hesse-Normalenform der Ebene

Die Hesse-Normalenform

E^{HNF}

einer Ebene

E

entsteht durch Teilung der Normalenform der Ebene

E

mit dem Betrag des Normalenvektors

| \vec{n_{E}} |

.

Beispiel:

E : x_{1} + 2 x_{2} + 2 x_{3} - 4 = 0

\vec{n_{E}} = (\begin{matrix} 1 \\ 2 \\ 2 \end{matrix})

\Rightarrow

| \vec{n_{E}} | = \sqrt{1 + 4 + 4} = 3

E^{HNF} : \frac{1}{3} \cdot (x_{1} + 2 x_{2} + 2 x_{3} - 4) = 0

E^{HNF} : \frac{1}{13} (12 x_{2} + 5 x_{3} - 60) = 0

Schritt einblenden / ausblenden

Abstand Ebene zu Geradenpunkt gleich 0,5 setzen:

Schritt einblenden / ausblenden

Abstand Punkt - Ebene

Durch Einsetzen der Koordinaten eines Punktes

P

in die Hesse-Normalenform

E^{HNF}

der Ebene

E

(zwischen Betragsstriche), bestimmt man den Abstand

d (P, E)

des Punktes zur Ebene.

Beispiel:

E^{HNF} : \frac{1}{3} \cdot (x_{1} + 2 x_{2} + 2 x_{3} - 4) = 0

P (1 | 3 | - 6)

d (P, E) = | \frac{1}{3} \cdot (1 + 2 \cdot 3 + 2 \cdot (- 6) - 4) | = | - \frac{9}{3} | = 3

In diesem Fall wird der allgemeine Geradenpunkt

(2, 5 | 2, 5 | 6 + λ)

eingesetzt.

| \frac{1}{13} (12 \cdot 2, 5 + 5 \cdot (6 + λ) - 60) | = 0, 5

| \frac{1}{13} (30 + 30 + 5 λ - 60) | = 0, 5

| \frac{1}{13} \cdot 5 λ | = 0, 5

| λ | = 0, 5 \cdot 13 \cdot \frac{1}{5} = 1, 3

λ = \pm 1, 3

Koordinaten der Lichtquelle bestimmen:

Schritt einblenden / ausblenden

Lage des Punktes

Die Lichtquelle liegt innerhalb des Zeltes, deswegen kann nur der Wert

λ = - 1, 3

richtig sein.

\vec{L} = (\begin{matrix} 2, 5 \\ 2, 5 \\ 6 \end{matrix}) - 1, 3 \cdot (\begin{matrix} 0 \\ 0 \\ 1 \end{matrix})

L (2, 5 | 2, 5 | 4, 7)

Alternative Lösung

weitere Abituraufgaben zu diesem Thema

Abstand zur Ebene

F

F : 12 x_{1} - 5 x_{3} = 0

\vec{n_{F}} = (\begin{matrix} 12 \\ 0 \\ - 5 \end{matrix})

Normalenvektor der Ebene

F

| \vec{n_{F}} | = 13

Hesse-Normalenform

F^{HNF}

der Ebene aufstellen:

F^{HNF} : \frac{1}{13} (12 x_{1} - 5 x_{3}) = 0

Abstand Ebene zu Geradenpunkt gleich 0,5 setzen:

| \frac{1}{13} (12 \cdot 2, 5 - 5 \cdot (6 + λ)) | = 0, 5

| \frac{1}{13} (30 - 30 - 5 λ) | = 0, 5

| - \frac{1}{13} \cdot 5 λ | = 0, 5

| - λ | = 0, 5 \cdot 13 \cdot \frac{1}{5} = 1, 3

λ = \pm 1, 3

Koordinaten der Lichtquelle bestimmen, indem

λ

in die Geradengleichung eingesetzt wird (vgl. vorherige Lösung).

Alle Abituraufgaben

Lösungen zu:

Teilaufgabe Teil A 1a

Teilaufgabe Teil A 1b

Teilaufgabe Teil A 2a

Teilaufgabe Teil A 2b

Teilaufgabe Teil B a

Teilaufgabe Teil B b

Teilaufgabe Teil B c

Teilaufgabe Teil B d

Teilaufgabe Teil B e

Teilaufgabe Teil B f

Lösung als Video:

Lösung als Video

Themen dieser Aufgabe:

Geradengleichung aufstellen

Abstand Punkt - Ebene

Alternative Lösung

Themen-Übersicht

Tipp:

Arbeite frühzeitig mit der Merkhilfe Mathematik,
die als Hilfsmittel im Abitur zugelassen ist.

Feedback:

Du hast einen Fehler gefunden oder hast Anregungen zur Internetseite?

Teile uns Dein Feedback mit!