über 250 kostenlose
Abituraufgaben
Lösung als Video
und ausformuliert
Alle Lösungen von
erfahrenen Lehrern
Abitur 2017 Mathematik Analytische Geometrie VI
Gegeben sind die beiden bezüglich der -Ebene symmetrisch liegenden Punkte und sowie der Punkt .
Teilaufgabe Teil A 1a (3 BE)
Weisen Sie nach, dass das Dreieck bei rechtwinklig ist.
Teilaufgabe Teil A 1b (2 BE)
Geben Sie die Koordinaten eines weiteren Punkts der -Achse an, so dass das Dreieck bei rechtwinklig ist. Begründen Sie Ihre Antwort.
Gegeben ist die Ebene .
Teilaufgabe Teil A 2a (2 BE)
Der Schnittpunkt von mit der -Achse, der Schnittpunkt von mit der -Achse und der Koordinatenursprung sind die Eckpunkte eines Dreiecks. Bestimmen Sie den Flächeninhalt dieses Dreiecks.
Teilaufgabe Teil A 2b (3 BE)
Ermitteln Sie die Koordinaten des Vektors, der sowohl ein Normalenvektor von als auch der Ortsvektor eines Punkts der Ebene ist.
| Ein geschlossenes Zelt, das auf horizontalem Untergrund steht, hat die Form einer Pyramide mit quadratischer Grundfläche. Die von der Zeltspitze ausgehenden Seitenkanten werden durch vier gleich lange Stangen gebildet. Das Zelt ist hoch, die Seitenlänge des Zeltbodens beträgt . Das Zelt wird in einem kartesischen Koordinatensystem (vgl. Abbildung 1) modellhaft durch eine Pyramide mit der Spitze dargestellt. Der Punkt liegt im Koordinatenursprung, hat die Koordinaten . Der Punkt liegt auf der -Achse, auf der -Achse. Das Dreieck liegt in der Ebene . Eine Längeneinheit im Koordinatensystem entspricht einem Meter in der Realität. |  |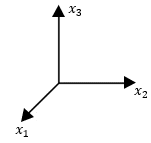
Teilaufgabe Teil B a (3 BE)
Geben Sie die Koordinaten der Punkte und an und zeichnen Sie die Pyramide in ein Koordinatensystem ein.
Teilaufgabe Teil B b (3 BE)
Ermitteln Sie eine Gleichung der Ebene , in der das Dreieck liegt, in Normalenform.
(mögliches Ergebnis: )
Teilaufgabe Teil B c (3 BE)
Jeweils zwei benachbarte Zeltwände schließen im Inneren des Zelts einen stumpfen Winkel ein. Ermitteln Sie die Größe dieses Winkels.
Teilaufgabe Teil B d (4 BE)
Im Zelt ist eine Lichtquelle so aufgehängt, dass sie von jeder der vier Wände einen Abstand von hat. Ermitteln Sie die Koordinaten des Punkts, der im Modell die Lichtquelle darstellt.
Teilaufgabe Teil B e (2 BE)
Bestimmen Sie eine Gleichung der Symmetrieachse des Dreiecks .
Teilaufgabe Teil B f (5 BE)
| Ein Teil der Zeltwand, die im Modell durch das Dreieck dargestellt wird, kann mithilfe zweier vertikal stehender Stangen der Länge zu einem horizontalen Vordach aufgespannt werden (vgl. Abbildung 2). Die dadurch entstehende breite Öffnung in der Zeltwand wird im Modell durch ein Rechteck dargestellt, das symmetrisch zu liegt. Dabei liegt eine Seite dieses Rechtecks auf der Strecke . Berechnen Sie den Flächeninhalt des Vordachs. |  |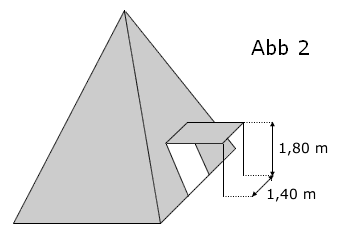
Lösungen zu:
Lösung als Video:
Themen-Übersicht
Tipp:
Arbeite frühzeitig mit der Merkhilfe Mathematik,
die als Hilfsmittel im Abitur zugelassen ist.
die als Hilfsmittel im Abitur zugelassen ist.
Feedback:
Du hast einen Fehler gefunden oder hast Anregungen zur Internetseite?
© 2001 - 2024 Abiturloesung.de. Alle Rechte vorbehalten.
