über 250 kostenlose
Abituraufgaben
Lösung als Video
und ausformuliert
Alle Lösungen von
erfahrenen Lehrern
 
 
 
 
Lösung Abitur Bayern 2010 Mathematik LK Stochastik IV


 
Teilaufgabe 1d  (7 BE)
Es werden zufällig 16 Bausteine aus der Kiste entnommen. Die beiden Säulendiagramme zeigen die Wahrscheinlichkeiten, dabei k gelbe Steine zu erhalten. Das linke Diagramm zeigt die zugehörige Binomialverteilung, das rechte ergibt sich bei Näherung durch die Normalverteilung.

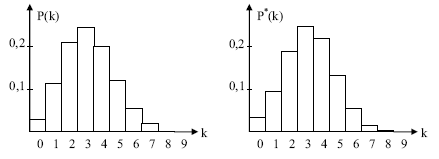
Prüfen Sie, ob das Kriterium für eine brauchbare Approximation der Binomialverteilung durch die Normalverteilung erfüllt ist (vgl. Formelsammlung). Zeigen Sie rechnerisch, dass es einen Wert für k gibt, bei dem die in den Diagrammen dargestellten Wahrscheinlichkeiten P ( k ) und P * ( k ) um mehr als 2 Prozentpunkte voneinander abweichen.
 
Lösung zu Teilaufgabe 1d

Standardabweichung einer Zufallsgröße



n = 16
p = P (gelb) = 0 , 2 (siehe Teilaufgabe 1a)
q = 1 - p = 0 , 8

Erwartungswert μ bestimmen:
μ = n ⋅ p = 16 ⋅ 0 , 2 = 3 , 2

Varianz σ 2 bestimmen:
σ 2 = n ⋅ p ⋅ q = 3 , 2 ⋅ 0 , 8 = 2 , 56

Standardabweichung σ bestimmen:
σ = 2 , 56 = 1 , 6 < 3


⇒ Keine Normalverteilung möglich.
Binomialverteilung



Wähle k = 2 .

Binomialverteilung:

P ( 2 ) = P 0 , 2 16 ( Z = 2 )
Schritt einblenden / ausblenden
= ( 16 2 ) ⋅ 0 , 2 2 ⋅ 0 , 8 14 = 0 , 2111
Normalverteilung



Normalverteilung als Approximation der Binomialverteilung:

P * ( Z = 2 )
Schritt einblenden / ausblenden
= φ ( 2 - 3 , 2 1 , 6 ) 1 , 6

= φ ( - 0 , 75 1 , 6 ) 1 , 6

= φ ( 0 , 75 1 , 6 ) 1 , 6

(Wert wird aus den Quantilen des stochastischen Tafelwerks entnommen)

= 0 , 30144 1 , 6 = 0 , 1884



Differenz:

P ( 2 ) - P * ( 2 ) = 0 , 2111 - 0 , 1884 = 0 , 0227 > 0 , 2


⇒ Für k = 2 weichen die Wahrscheinlichkeiten P ( k ) und P * ( k ) um mehr als 2 Prozentpunkte voneinander ab.

Themen-Übersicht
Themen
Tipp:
Arbeite frühzeitig mit der Merkhilfe Mathematik,
die als Hilfsmittel im Abitur zugelassen ist.
Feedback:
Du hast einen Fehler gefunden oder hast Anregungen zur Internetseite?