Lösung Abitur Bayern 2009 Mathematik LK Infinitesimalrechnung II

zur Angabe dieser Abituraufgabe

Teilaufgabe 1a (3 BE)

Gegeben ist die Schar der Funktionen

f_{a} : x \mapsto a^{3} x^{2} e^{- a x}

mit

a \in ℝ^{+}

und der Definitionsmenge

ℝ

. Der Graph von

f_{a}

wird mit

G_{a}

bezeichnet. Die Abbildung zeigt

G_{a}

für

a = 0, 04

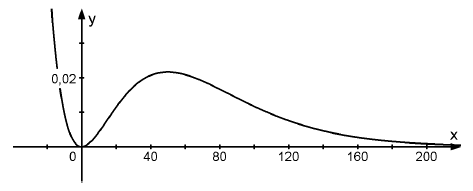
Untersuchen Sie am Funktionsterm das Verhalten von

f_{a}

für

x \to - \infty

und für

x \to + \infty

. Begründen Sie, dass

G_{a}

nie unterhalb der

x

-Achse verläuft.

Lösung zu Teilaufgabe 1a

Verhalten der Funktion an den Rändern des Definitionsbereichs

weitere Abituraufgaben zu diesem Thema

f_{a} (x) = a^{3} x^{2} e^{- a x}, a \in ℝ^{+}, x \in ℝ

Limes gegen

- \infty

lim_{x \to - \infty} f_{a} (x) = lim_{x \to - \infty} \overset{\to + \infty}{\overset{︷}{\underset{> 0}{\underset{︸}{a^{3}}} x^{2}}} \underset{\to + \infty}{\underset{︸}{e^{- a x}}} = + \infty

Limes gegen

+ \infty

lim_{x \to + \infty} f_{a} (x) = lim_{x \to + \infty} \overset{\to + \infty}{\overset{︷}{\underset{> 0}{\underset{︸}{a^{3}}} x^{2}}} \underset{\to 0^{+}}{\underset{︸}{e^{- a x}}}

= lim_{x \to + \infty} a^{3} \frac{\overset{\to + \infty}{\overset{︷}{x^{2}}}}{\underset{\to + \infty}{\underset{︸}{e^{a x}}}}

Schritt einblenden / ausblenden

L’Hospitalsche Regel

Liegt bei

\lim_{x \to x_{0}} \frac{f (x)}{g (x)}

ein "unbestimmter Ausdruck" des Typs "

\frac{0}{0}

" oder "

\frac{\infty}{\infty}

", dann besagt die Regel von l'Hospital dass:

\lim_{x \to x_{0}} \frac{f (x)}{g (x)} = \lim_{x \to x_{0}} \frac{f^{'} (x)}{g^{'} (x)}

In diesem Fall wird die Regel zweimal angewendet.

= lim_{x \to + \infty} a^{3} \frac{\overset{\to + \infty}{\overset{︷}{2 x}}}{\underset{\to + \infty}{\underset{︸}{a e^{a x}}}}

= lim_{x \to + \infty} a^{3} \frac{2}{\underset{\to + \infty}{\underset{︸}{a^{2} e^{a x}}}}

= 0^{+}

Schnittpunkte mit den Koordinatenachsen

weitere Abituraufgaben zu diesem Thema

Begründung:

f_{a} (x) = \underset{> 0}{\underset{︸}{a^{3}}} \overset{\geq 0}{\overset{︷}{x^{2}}} \underset{> 0}{\underset{︸}{e^{- a x}}} \geq 0

\Rightarrow G_{a}

verläuft nie unterhalb der

x

-Achse, da

f_{a} (x)

größer gleich Null ist für alle

x \in D_{f_{a}}

Alle Abituraufgaben

Lösungen zu:

Teilaufgabe 1a

Teilaufgabe 1b

Teilaufgabe 2a

Teilaufgabe 2b

Teilaufgabe 2c

Teilaufgabe 3a

Teilaufgabe 3b

Lösung als Video:

Lösung als Video

Themen dieser Aufgabe:

Verhalten der Funktion an den Rändern des Definitionsbereichs

Schnittpunkte mit den Koordinatenachsen

Themen-Übersicht

Tipp:

Arbeite frühzeitig mit der Merkhilfe Mathematik,
die als Hilfsmittel im Abitur zugelassen ist.

Feedback:

Du hast einen Fehler gefunden oder hast Anregungen zur Internetseite?

Teile uns Dein Feedback mit!