über 250 kostenlose
Abituraufgaben
Lösung als Video
und ausformuliert
Alle Lösungen von
erfahrenen Lehrern
 
 
 
 
AB SOFORT: KEIN LOGIN mehr erforderlich - alle Lösungen zu den Abituraufgaben sind frei zugänglich.
 

Abitur 2009 Mathematik LK Infinitesimalrechnung II

Gegeben ist die Schar der Funktionen f a : x ↦ a 3 x 2 e - a x mit a ∈ ℝ + und der Definitionsmenge ℝ . Der Graph von f a wird mit G a bezeichnet. Die Abbildung zeigt G a für a = 0 , 04 .

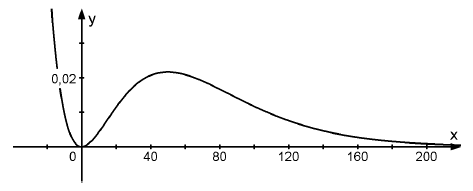
Teilaufgabe 1a  (3 BE)

Untersuchen Sie am Funktionsterm das Verhalten von f a für x → - ∞ und für x → + ∞ . Begründen Sie, dass G a nie unterhalb der x -Achse verläuft.

Teilaufgabe 1b  (7 BE)

Bestimmen Sie Art und Lage der Extrempunkte von G a .
[Zur Kontrolle: Tiefpunkt bei x = 0 und Hochpunkt bei x = 2 a ]

Nun werden die in ℝ definierten Integralfunktionen F a : x ↦ ∫ 0 x f a ( t ) d t betrachtet.
Teilaufgabe 2a  (4 BE)

Begründen Sie ohne Ausführung der Integration, dass der Graph von F a für alle a ∈ ℝ + durch den Koordinatenursprung verläuft und dort einen Terrassenpunkt besitzt.

Teilaufgabe 2b  (10 BE)

Berechnen Sie durch partielle Integration einen integralfreien Term für F a . Geben Sie den Grenzwert von F a für x → + ∞ an und interpretieren Sie das Ergebnis am Graphen G a .
[Teilergebnis: F a ( x ) = 2 - e - a x ⋅ ( a 2 x 2 + 2 a x + 2 ) ]

Teilaufgabe 2c  (6 BE)

Nun sei a = 0 , 04 . Der Graph der Funktion F 0 , 04 besitzt für x > 0 einen Wendepunkt W . Bestimmen Sie die Koordinaten von W .
Skizzieren Sie unter Berücksichtigung der bisherigen Ergebnisse den Graphen von F 0 , 04 im Bereich - 30 ≤ x ≤ 200 in ein Koordinatensystem ( x -Achse: 50 LE = 2,5 cm, y -Achse: 1 LE = 2,5 cm). Verwenden Sie dazu ohne Nachweis: F 0 , 04 ( - 30 ) ≈ - 1 , 45 und F 0 , 04 ( 200 ) ≈ 1 , 97 .

Die Gruppe "Die toten Rosen" gibt ein Konzert. Es beginnt um 20 Uhr, der Einlass wird ab 18 Uhr gewährt. Der Besucherzustrom soll durch eine Funktion g der Form g ( x ) = k ⋅ f a ( x ) mit geeignetem a und geeignetem k > 0 modelliert werden. Dabei bedeutet x die seit 18 Uhr vergangene Zeit in Minuten. g ( x ) gibt die momentane Zunahme der Besucherzahl in Besucher pro Minute an.
Teilaufgabe 3a  (5 BE)

Bestimmen Sie die Parameter a und k , wenn das Maximum der Funktion g um 18.50 Uhr auftritt und 26 Besucher pro Minute beträgt.

Teilaufgabe 3b  (5 BE)

Berechnen Sie für a = 0 , 04 und k = 1200 unter Verwendung des in Teilaufgabe 2b ermittelten Terms F a ( x ) das Integral ∫ 0 120 g ( x ) d x und interpretieren Sie das Ergebnis im Anwendungszusammenhang.

Lösung als Video:

 
Themen-Übersicht
Themen
Tipp:
Arbeite frühzeitig mit der Merkhilfe Mathematik,
die als Hilfsmittel im Abitur zugelassen ist.
Feedback:
Du hast einen Fehler gefunden oder hast Anregungen zur Internetseite?