über 250 kostenlose
Abituraufgaben
Lösung als Video
und ausformuliert
Alle Lösungen von
erfahrenen Lehrern
Abitur 2014 Mathematik Analytische Geometrie VI
| Die Vektoren , und spannen für jeden Wert von mit einen Körper auf. Die Abbildung zeigt den Sachverhalt beispielhaft für einen Wert von . | 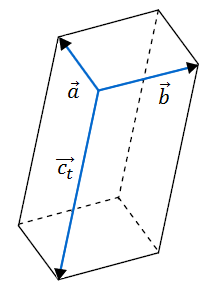 |
Teilaufgabe Teil A 1a (2 BE)
Zeigen Sie, dass die aufgespannten Körper Quader sind.
Teilaufgabe Teil A 1b (3 BE)
Bestimmen Sie diejenigen Werte von , für die der jeweils zugehörige Quader das Volumen besitzt.
Eine Kugel besitzt den Mittelpunkt . Der Punkt liegt auf der Kugel.
Teilaufgabe Teil A 2a (3 BE)
Der Punkt liegt ebenfalls auf der Kugel, die Strecke verläuft durch deren Mittelpunkt. Ermitteln Sie die Koordinaten von .
Teilaufgabe Teil A 2b (2 BE)
Weisen Sie nach, dass die Kugel die -Ebene berührt.
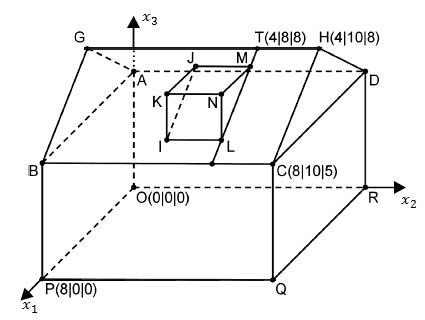
Die Abbildung zeigt modellhaft ein Einfamilienhaus, das auf einer horizontalen Fläche steht. Auf einer der beiden rechteckigen Dachflächen soll eine Dachgaube errichtet werden. Die Punkte , , , , , , und sind die Eckpunkte eines Quaders. Das gerade dreiseitige Prisma stellt die Dachgaube dar, die Strecke den First des Dachs, d. h. die obere waagrechte Dachkante. Eine Längeneinheit im Koordinatensystem entspricht m, d. h. das Haus ist m lang.

Teilaufgabe Teil B a (2 BE)
Berechnen Sie den Inhalt derjenigen Dachfläche, die im Modell durch das Rechteck dargestellt wird.
Teilaufgabe Teil B b (3 BE)
In der Stadt, in der das Einfamilienhaus steht, gilt für die Errichtung von Dachgauben eine Satzung, die jeder Bauherr einhalten muss. Diese Satzung lässt die Errichtung einer Dachgaube zu, wenn die Größe des Neigungswinkels der Dachfläche des jeweiligen Hausdachs gegen die Horizontale mindestens beträgt. Zeigen Sie rechnerisch, dass für das betrachtete Einfamilienhaus die Errichtung einer Dachgaube zulässig ist.
Die Dachfläche, auf der die Dachgaube errichtet wird, liegt im Modell in der Ebene .
Die Dachgaube soll so errichtet werden, dass sie von dem seitlichen Rand der Dachfläche, der im Modell durch die Strecke dargestellt wird, den Abstand m und vom First des Dachs den Abstand m hat. Zur Ermittlung der Koordinaten des Punkts wird die durch den Punkt verlaufende Gerade , , betrachtet.
Die Dachgaube soll so errichtet werden, dass sie von dem seitlichen Rand der Dachfläche, der im Modell durch die Strecke dargestellt wird, den Abstand m und vom First des Dachs den Abstand m hat. Zur Ermittlung der Koordinaten des Punkts wird die durch den Punkt verlaufende Gerade , , betrachtet.
Teilaufgabe Teil B c (5 BE)
Begründen Sie, dass in der Ebene verläuft und von der Geraden den Abstand besitzt.
Teilaufgabe Teil B d (3 BE)
Auf der Geraden wird nun der Punkt so festgelegt, dass der Abstand der Dachgaube vom First m beträgt. Bestimmen Sie die Koordinaten von .
( Ergebnis: )
Die Punkte und liegen auf der Geraden , , die im Modell die Neigung der Dachfläche der Gaube festlegt. Die zur -Achse parallele Strecke stellt im Modell den sogenannten Gaubenstiel dar; dessen Länge soll m betragen. Um die Koordinaten von und zu bestimmen, wird die Ebene betrachtet, die durch Verschiebung von um in positive -Richtung entsteht.
Teilaufgabe Teil B e (3 BE)
Begründen Sie, dass eine Gleichung von ist.
Teilaufgabe Teil B f (4 BE)
Bestimmen Sie die Koordinaten von und .
( Teilergebnis: )
Lösungen zu:
Tipp:
Arbeite frühzeitig mit der Merkhilfe Mathematik,
die als Hilfsmittel im Abitur zugelassen ist.
die als Hilfsmittel im Abitur zugelassen ist.
Feedback:
Du hast einen Fehler gefunden oder hast Anregungen zur Internetseite?








