über 250 kostenlose
Abituraufgaben
Lösung als Video
und ausformuliert
Alle Lösungen von
erfahrenen Lehrern
 
 
 
 
AB SOFORT: KEIN LOGIN mehr erforderlich - alle Lösungen zu den Abituraufgaben sind frei zugänglich.
 

Abitur 2008 Mathematik GK Infinitesimalrechnung II

Die Abbildung zeigt den Graphen G g der Funktion g : x ↦ ( 4 x - 2 ) ⋅ e 2 x mit dem Definitionsbereich D g = ℝ .

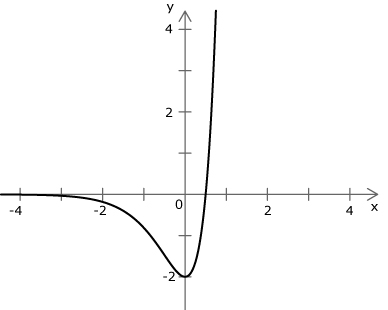
Teilaufgabe 1a  (5 BE)

Berechnen Sie die Nullstellen von g .
G g besitzt genau einen Tiefpunkt (Nachweis nicht erforderlich).
Berechnen Sie dessen Koordinaten. [Zur Kontrolle: g ′ ( x ) = 8 x e 2 x ]

Teilaufgabe 1b  (9 BE)

Weisen Sie nach, dass G g genau einen Wendepunkt besitzt, und bestimmen Sie die Gleichung der Wendetangente w . Tragen Sie diese in obige Abbildung ein. [Zur Kontrolle: w : y = - 4 e x - 6 e ]

Teilaufgabe 1c  (5 BE)

Gegeben ist die Integralfunktion I : x ↦ ∫ 0 x g ( t ) d t mit x ∈ ℝ .
Für verschiedene Werte von x wird jeweils das Vorzeichen von I ( x ) betrachtet. Was kann hierüber ohne Rechnung im Bereich 0 < x ≤ 0 , 5 ausgesagt werden, was im Bereich x > 0 , 5 ? Begründen Sie Ihre Antwort, ohne eine integralfreie Darstellung von I zu verwenden.

Gegeben ist zusätzlich die Funktion h : x ↦ ( - 4 x - 2 ) ⋅ e - 2 x mit Definitionsbereich D h = ℝ und zugehörigem Graph G h .
Teilaufgabe 2a  (6 BE)

Begründen Sie anhand der Funktionsterme von g und h , dass man G h erhält, indem man G g an der y -Achse spiegelt. Zeichnen Sie G h in die Abbildung ein.
Geben Sie die Gleichung der Wendetangente von G h an.

Teilaufgabe 2b  (5 BE)

Die Funktion G : x ↦ ( 2 x - 2 ) ⋅ e 2 x mit D G = ℝ ist eine Stammfunktion von g (Nachweis nicht erforderlich). Die Schnittpunkte der Graphen G g bzw. G h mit der x -Achse werden mit N bzw. M bezeichnet.
Berechnen Sie den Inhalt A des Flächenstücks, das von der Strecke [ M N ] sowie den Graphen G g und G h eingeschlossen wird.
(Hinweis: G g und G h schneiden sich nur auf der y -Achse.)

Betrachtet wird nun die Schar der in ℝ definierten Funktionen f a : x ↦ ( 2 a x - 2 ) ⋅ e a x mit a ∈ ℝ ∖ { 0 } .
Teilaufgabe 3a  (3 BE)

Zeigen Sie, dass die Funktionen g und h Funktionen der Schar sind, indem Sie die zugehörigen Parameterwerte a angeben.
Weisen Sie nach, dass alle Graphen der Schar die y -Achse im selben Punkt schneiden.

Teilaufgabe 3b  (3 BE)

Jede Funktion der Schar hat genau eine Wendestelle und zwar bei x = - 1 a (Nachweis nicht erforderlich). Zeigen Sie, dass alle Wendepunkte auf einer Parallelen p zur x -Achse liegen, und geben Sie die Gleichung von p an.

Teilaufgabe 3c  (4 BE)

Die Wendetangente jedes Graphen der Schar schließt mit den Koordinatenachsen ein rechtwinkliges Dreieck ein. Für bestimmte Werte von a ist dieses Dreieck gleichschenklig.
Beschreiben Sie einen Weg, um diese Werte von a rechnerisch zu ermitteln (Rechnungen nicht erforderlich).

Lösung als Video:

 
Themen-Übersicht
Themen
Tipp:
Arbeite frühzeitig mit der Merkhilfe Mathematik,
die als Hilfsmittel im Abitur zugelassen ist.
Feedback:
Du hast einen Fehler gefunden oder hast Anregungen zur Internetseite?