über 250 kostenlose
Abituraufgaben
Lösung als Video
und ausformuliert
Alle Lösungen von
erfahrenen Lehrern
Abitur 2016 Mathematik Stochastik III
Teilaufgabe Teil A 1 (5 BE)
Die beiden Baumdiagramme gehören zum selben Zufallsexperiment mit den Ereignissen und .
Berechnen Sie die Wahrscheinlichkeit und ergänzen Sie anschließend an allen Ästen des rechten Baumdiagramms die zugehörigen Wahrscheinlichkeiten.
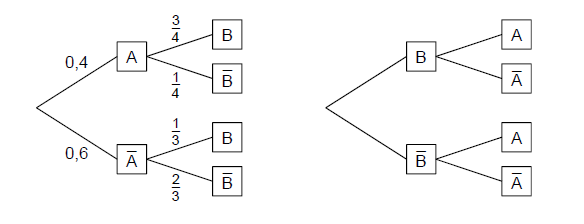
(Teilergebnis: )
Berechnen Sie die Wahrscheinlichkeit und ergänzen Sie anschließend an allen Ästen des rechten Baumdiagramms die zugehörigen Wahrscheinlichkeiten.

(Teilergebnis: )
Bei einem Zufallsexperiment wird eine ideale Münze so lange geworfen, bis zum zweiten Mal Zahl () oder zum zweiten Mal Wappen () oben liegt. Als Ergebnismenge wird festgelegt: .
Teilaufgabe Teil A 2a (2 BE)
Begründen Sie, dass dieses Zufallsexperiment kein Laplace-Experiment ist.
Teilaufgabe Teil A 2b (3 BE)
Die Zufallsgröße ordnet jedem Ergebnis die Anzahl der entsprechenden Münzwürfe zu. Berechnen Sie den Erwartungswert von .
Ein Getränkehersteller führt eine Werbeaktion durch, um die Verkaufszahlen seiner Saftschorlen zu erhöhen. Bei 100000 der für die Werbeaktion produzierten zwei Millionen Flaschen wird auf der Innenseite des Verschlusses eine Marke für einen Geldgewinn angebracht. Von den Gewinnmarken sind 12000 jeweils 5 € wert, der Rest ist jeweils 1 € wert. Alle Flaschen der Werbeaktion werden zufällig auf Kästen verteilt. Im Folgenden werden nur Flaschen aus der Werbeaktion betrachtet.
Es wird eine Flasche geöffnet. Betrachtet werden folgende Ereignisse:
: "Der Verschluss enthält eine Gewinnmarke."
: "Der Verschluss enthält eine Gewinnmarke im Wert von 1 €."
: "Der Verschluss enthält eine Gewinnmarke."
: "Der Verschluss enthält eine Gewinnmarke im Wert von 1 €."
Teilaufgabe Teil B 1a (2 BE)
Berechnen Sie die Wahrscheinlichkeiten und .
Teilaufgabe Teil B 1b (2 BE)
Es werden mehrere Flaschen geöffnet und für jede dieser Flaschen wird festgestellt, ob das Ereignis eintritt. Begründen Sie, dass dieses Zufallsexperiment näherungsweise durch eine Bernoullikette beschrieben werden kann.
Im Folgenden gilt beim Öffnen einer Flasche stets und .
Teilaufgabe Teil B 1c (2 BE)
Es werden nacheinander zehn Flaschen geöffnet. Berechnen Sie die Wahrscheinlichkeit dafür, dass sich erstmals in der fünften Flasche eine Gewinnmarke befindet.
Teilaufgabe Teil B 1d (4 BE)
Bestimmen Sie unter Zuhilfenahme des Tafelwerks, wie viele Flaschen man mindestens öffnen muss, um mit einer Wahrscheinlichkeit von mehr als mindestens zwei Gewinnmarken zu finden.
Teilaufgabe Teil B 1e (3 BE)
Berechnen Sie den Gesamtwert der Gewinnmarken, die Kunden beim Öffnen der 20 Flaschen eines Kastens im Mittel in den Verschlüssen finden.
Nachdem die zwei Millionen Flaschen verkauft sind, wird die Werbeaktion fortgesetzt. Der Getränkehersteller verspricht, dass weiterhin jede 20. Flasche eine Gewinnmarke enthält. Aufgrund von Kundenäußerungen vermutet der Filialleiter eines Getränkemarkts jedoch, dass der Anteil der Saftschorle-Flaschen mit einer Gewinnmarke im Verschluss nun geringer als 0,05 ist, und beschwert sich beim Getränkehersteller.
Teilaufgabe Teil B 2 (7 BE)
Der Getränkehersteller bietet ihm an, anhand von 200 zufällig ausgewählten Flaschen einen Signifikanztest für die Nullhypothese "Die Wahrscheinlichkeit dafür, in einer Flasche eine Gewinnmarke zu finden, beträgt mindestens ." auf einem Signifikanzniveau von durchzuführen. Für den Fall, dass das Ergebnis des Tests im Ablehnungsbereich der Nullhypothese liegt, verspricht der Getränkehersteller, seine Abfüllanlage zu überprüfen und die Kosten für eine Sonderwerbeaktion des Getränkemarkts zu übernehmen.
Ermitteln Sie den Ablehnungsbereich der Nullhypothese und bestimmen Sie anschließend unter der Annahme, dass im Mittel nur der Saftschorle-Flaschen eine Gewinnmarke enthalten, die Wahrscheinlichkeit dafür, dass der Getränkemarkt nicht in den Genuss einer kostenlosen Sonderwerbeaktion kommt.
Ermitteln Sie den Ablehnungsbereich der Nullhypothese und bestimmen Sie anschließend unter der Annahme, dass im Mittel nur der Saftschorle-Flaschen eine Gewinnmarke enthalten, die Wahrscheinlichkeit dafür, dass der Getränkemarkt nicht in den Genuss einer kostenlosen Sonderwerbeaktion kommt.
Lösungen zu:
Tipp:
Arbeite frühzeitig mit der Merkhilfe Mathematik,
die als Hilfsmittel im Abitur zugelassen ist.
die als Hilfsmittel im Abitur zugelassen ist.
Feedback:
Du hast einen Fehler gefunden oder hast Anregungen zur Internetseite?








