Lösung Abitur Bayern 2016 Mathematik Infinitesimalrechnung II

zur Angabe dieser Abituraufgabe

Teilaufgabe Teil B 1a (6 BE)

Im Rahmen eines W-Seminars modellieren Schülerinnen und Schüler einen Tunnelquerschnitt, der senkrecht zum Tunnelverlauf liegt. Dazu beschreiben sie den Querschnitt der Tunnelwand durch den Graphen einer Funktion in einem Koordinatensystem. Der Querschnitt des Tunnelbodens liegt dabei auf der x-Achse, sein Mittelpunkt M im Ursprung des Koordinatensystems; eine Längeneinheit im Koordinatensystem entspricht einem Meter in der Realität. Für den Tunnelquerschnitt sollen folgende Bedingungen gelten:

I Breite des Tunnelbodens: b = 10 m

II Höhe des Tunnels an der höchsten Stelle: h = 5 m

III Der Tunnel ist auf einer Breite von mindestens 6 m mindestens 4 m hoch.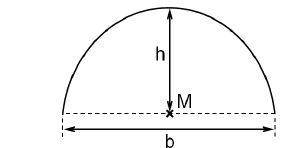

Eine erste Modellierung des Querschnitts der Tunnelwand verwendet die Funktion

p : x \mapsto - 0, 2 x^{2} + 5

mit Definitionsbereich

D_{p}

= [-5;5].

Zeigen Sie, dass die Bedingungen I und II in diesem Modell erfüllt sind.
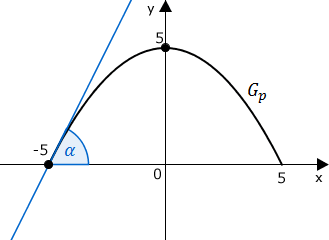
Berechnen Sie die Größe des spitzen Winkels, unter dem bei dieser Modellierung die linke Tunnelwand auf den Tunnelboden trifft.

Lösung zu Teilaufgabe Teil B 1a

Nullstellen einer Funktion

weitere Abituraufgaben zu diesem Thema

p (x) = - 0, 2 x^{2} + 5

Schritt einblenden / ausblenden

Nullstellen

Der Ansatz, um die Nullstellen (die Schnittpunkte einer Funktion

f

mit der

x

-Achse) zu bestimmen, lautet stets:

f (x) = 0

Die Gleichung muss anschließend nach

x

aufgelöst werden.

Nullstellen bestimmen:

p (x) = 0

0 = - 0, 2 x^{2} + 5

0, 2 x^{2} = 5

x^{2} = 25

\Rightarrow

x_{1, 2} = \pm \sqrt{25} = \pm 5

\Rightarrow

Bedingung I erfüllt

Scheitelpunktform einer Parabel

weitere Abituraufgaben zu diesem Thema

S (0 | 5)

ist Scheitelpunkt von

G_{p}

\Rightarrow

Bedingung II erfüllt

Winkel bestimmen

weitere Abituraufgaben zu diesem Thema

Erste Ableitung bestimmen:

p^{'} (x) = - 0, 4 x

Schritt einblenden / ausblenden

Tangentensteigung

Die Steigung der Tangente an den Graphen einer Funktion an der Stelle

x_{0}

, ist gleich dem Wert der ersten Ableitung der Funktion an der Stelle

x_{0}

.

Sie entspricht auch dem Tangens des Winkels

α

, welcher die Tangente mit der

x

-Achse bildet.

f^{'} (x_{0}) = \tan α

\tan α = p^{'} (- 5)

\tan α = 2

α = \tan^{- 1} (2) \approx 63, 4^{\circ}

Alle Abituraufgaben

Lösungen zu:

Teilaufgabe Teil A 1a

Teilaufgabe Teil A 1b

Teilaufgabe Teil A 2a

Teilaufgabe Teil A 2b

Teilaufgabe Teil A 3a

Teilaufgabe Teil A 3b

Teilaufgabe Teil A 3c

Teilaufgabe Teil A 4

Teilaufgabe Teil B 1a

Teilaufgabe Teil B 1b

Teilaufgabe Teil B 1c

Teilaufgabe Teil B 2a

Teilaufgabe Teil B 2b

Teilaufgabe Teil B 3a

Teilaufgabe Teil B 3b

Teilaufgabe Teil B 3c

Teilaufgabe Teil B 3d

Teilaufgabe Teil B 3e

Lösung als Video:

Lösung als Video

Themen dieser Aufgabe:

Nullstellen einer Funktion

Scheitelpunktform einer Parabel

Winkel bestimmen

Themen-Übersicht

Tipp:

Arbeite frühzeitig mit der Merkhilfe Mathematik,
die als Hilfsmittel im Abitur zugelassen ist.

Feedback:

Du hast einen Fehler gefunden oder hast Anregungen zur Internetseite?

Teile uns Dein Feedback mit!