über 250 kostenlose
Abituraufgaben
Lösung als Video
und ausformuliert
Alle Lösungen von
erfahrenen Lehrern
Abitur 2016 Mathematik Infinitesimalrechnung II
Gegeben ist die Funktion mit maximalem Definitionsbereich .
Teilaufgabe Teil A 1a (3 BE)
Geben Sie sowie die Nullstelle von an und bestimmen Sie .
Teilaufgabe Teil A 1b (4 BE)
Ermitteln Sie die -Koordinate des Punkts, in dem der Graph von eine waagrechte Tangente hat.
Geben Sie jeweils den Term und den Definitionsbereich einer Funktion an, die die angegebene(n) Eigenschaft(en) besitzt.
Teilaufgabe Teil A 2a (2 BE)
Der Punkt ist ein Wendepunkt des Graphen von .
Teilaufgabe Teil A 2b (2 BE)
Der Graph der Funktion ist streng monoton fallend und rechtsgekrümmt.
Abbildung 1 zeigt den Graphen der in definierten Funktion .
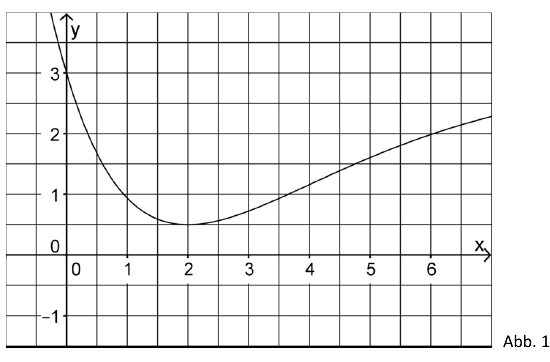

Teilaufgabe Teil A 3a (2 BE)
Bestimmen Sie mithilfe der Abbildung 1 einen Näherungswert für .
Die Funktion ist die in definierte Stammfunktion von mit .
Teilaufgabe Teil A 3b (1 BE)
Geben Sie mithilfe der Abbildung einen Näherungswert für die Ableitung von an der Stelle an.
Teilaufgabe Teil A 3c (2 BE)
Zeigen Sie, dass mit gilt.
Teilaufgabe Teil A 4 (4 BE)
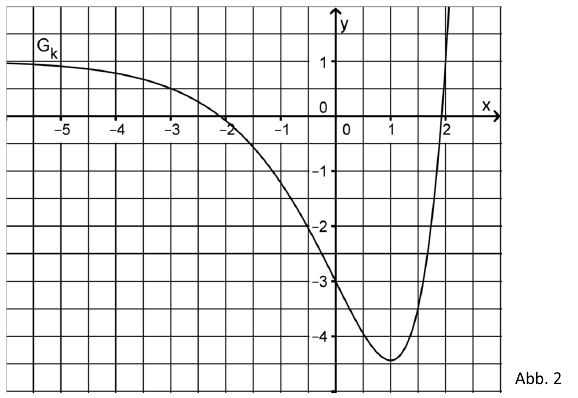
Abbildung 2 zeigt den Graphen einer in definierten Funktion .
Skizzieren Sie in Abbildung 2 den Graphen der zugehörigen Ableitungsfunktion . Berücksichtigen Sie dabei insbesondere einen Näherungswert für die Steigung des Graphen an dessen Wendepunkt sowie die Nullstelle von k'.
Skizzieren Sie in Abbildung 2 den Graphen der zugehörigen Ableitungsfunktion . Berücksichtigen Sie dabei insbesondere einen Näherungswert für die Steigung des Graphen an dessen Wendepunkt sowie die Nullstelle von k'.

Im Rahmen eines W-Seminars modellieren Schülerinnen und Schüler einen Tunnelquerschnitt, der senkrecht zum Tunnelverlauf liegt. Dazu beschreiben sie den Querschnitt der Tunnelwand durch den Graphen einer Funktion in einem Koordinatensystem. Der Querschnitt des Tunnelbodens liegt dabei auf der x-Achse, sein Mittelpunkt M im Ursprung des Koordinatensystems; eine Längeneinheit im Koordinatensystem entspricht einem Meter in der Realität. Für den Tunnelquerschnitt sollen folgende Bedingungen gelten:
| I Breite des Tunnelbodens: b = 10 m II Höhe des Tunnels an der höchsten Stelle: h = 5 m III Der Tunnel ist auf einer Breite von mindestens 6 m mindestens 4 m hoch. | 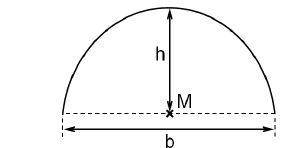 |
Eine erste Modellierung des Querschnitts der Tunnelwand verwendet die Funktion mit Definitionsbereich = [-5;5].
Teilaufgabe Teil B 1a (6 BE)
Zeigen Sie, dass die Bedingungen I und II in diesem Modell erfüllt sind.
Berechnen Sie die Größe des spitzen Winkels, unter dem bei dieser Modellierung die linke Tunnelwand auf den Tunnelboden trifft.
Berechnen Sie die Größe des spitzen Winkels, unter dem bei dieser Modellierung die linke Tunnelwand auf den Tunnelboden trifft.
Schülerinnen und Schüler untersuchen nun den Abstand der Graphenpunkte vom Ursprung des Koordinatensystems.
Teilaufgabe Teil B 1b (3 BE)
Zeigen Sie, dass gilt.
Teilaufgabe Teil B 1c (5 BE)
Es gibt Punkte des Querschnitts der Tunnelwand, deren Abstand zu minimal ist. Bestimmen Sie die x-Koordinaten der Punkte , für die minimal ist, und geben Sie davon ausgehend diesen minimalen Abstand an.
Eine zweite Modellierung des Querschnitts der Tunnelwand verwendet eine Kosinusfunktion vom Typ mit und Definitionsbereich , bei der offensichtlich Bedingung II erfüllt ist.
Teilaufgabe Teil B 2a (5 BE)
Bestimmen Sie so, dass auch Bedingung I erfüllt ist, und berechnen Sie damit den Inhalt der Querschnittsfläche des Tunnels.
(zur Kontrolle: , Inhalt der Querschnittsfläche: )
(zur Kontrolle: , Inhalt der Querschnittsfläche: )
Teilaufgabe Teil B 2b (2 BE)
Zeigen Sie, dass Bedingung III weder bei einer Modellierung mit aus Aufgabe 1 noch bei einer Modellierung mit erfüllt ist.
Eine dritte Modellierung des Querschnitts der Tunnelwand, bei der ebenfalls die Bedingungen I und II erfüllt sind, verwendet die Funktion mit Definitionsbereich .
Teilaufgabe Teil B 3a (5 BE)
Begründen Sie, dass in diesem Modell jeder Punkt des Querschnitts der Tunnelwand von der Bodenmitte den Abstand 5 m hat.
Zeichnen Sie den Graphen von in ein Koordinatensystem ein (Platzbedarf im Hinblick auf spätere Aufgaben: , ) und begründen Sie, dass bei dieser Modellierung auch Bedingung III erfüllt ist.
Zeichnen Sie den Graphen von in ein Koordinatensystem ein (Platzbedarf im Hinblick auf spätere Aufgaben: , ) und begründen Sie, dass bei dieser Modellierung auch Bedingung III erfüllt ist.
Betrachtet wird nun die Integralfunktion mit Definitionsbereich .
Teilaufgabe Teil B 3b (5 BE)
Zeigen Sie mithilfe einer geometrischen Überlegung, dass gilt.
Einer der Graphen A, B und C ist der Graph von . Entscheiden Sie, welcher dies ist, und begründen Sie Ihre Entscheidung, indem Sie erklären, warum die beiden anderen Graphen nicht infrage kommen.
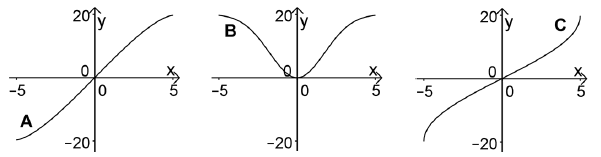
Einer der Graphen A, B und C ist der Graph von . Entscheiden Sie, welcher dies ist, und begründen Sie Ihre Entscheidung, indem Sie erklären, warum die beiden anderen Graphen nicht infrage kommen.

Teilaufgabe Teil B 3c (2 BE)
Berechnen Sie, um wie viel Prozent der Inhalt der Querschnittsfläche des Tunnels bei einer Modellierung mit von dem in Aufgabe 2a berechneten Wert abweicht.
Der Tunnel soll durch einen Berg führen. Im betrachteten Querschnitt wird das Profil des Berghangs über dem Tunnel durch eine Gerade mit der Gleichung modelliert.
Teilaufgabe Teil B 3d (4 BE)
Zeigen Sie, dass die Tangente an den Graphen von im Punkt parallel zu verläuft. Zeichnen Sie und in das Koordinatensystem aus Aufgabe 3a ein.
Teilaufgabe Teil B 3e (3 BE)
Der Punkt aus Aufgabe 3d entspricht demjenigen Punkt der Tunnelwand, der im betrachteten Querschnitt vom Hangprofil den kleinsten Abstand in Metern hat. Beschreiben Sie die wesentlichen Schritte eines Verfahrens zur rechnerischen Ermittlung von .
Lösungen zu:
Tipp:
Arbeite frühzeitig mit der Merkhilfe Mathematik,
die als Hilfsmittel im Abitur zugelassen ist.
die als Hilfsmittel im Abitur zugelassen ist.
Feedback:
Du hast einen Fehler gefunden oder hast Anregungen zur Internetseite?








