Abitur 2015 Mathematik Stochastik IV

In einer Urne befinden sich vier rote und sechs blaue Kugeln. Aus dieser wird achtmal eine Kugel zufällig gezogen, die Farbe notiert und die Kugel anschließend wieder zurückgelegt.

Teilaufgabe Teil A 1a (2 BE)

Geben Sie einen Term an, mit dem die Wahrscheinlichkeit des Ereignisses "Es werden gleich viele rote und blaue Kugeln gezogen." berechnet werden kann.

Teilaufgabe Teil A 1b (3 BE)

Beschreiben Sie im Sachzusammenhang jeweils ein Ereignis, dessen Wahrscheinlichkeit durch den angegebenen Term berechnet werden kann.

α)

1 - {(\frac{3}{5})}^{8}

β)

{(\frac{3}{5})}^{8} + 8 \cdot \frac{2}{5} \cdot {(\frac{3}{5})}^{7}

Für ein Zufallsexperiment wird eine Zufallsgröße

X

festgelegt, welche die drei Werte

- 2, 1

und

2

annehmen kann. In der Abbildung ist die Wahrscheinlichkeitsverteilung von

X

dargestellt.

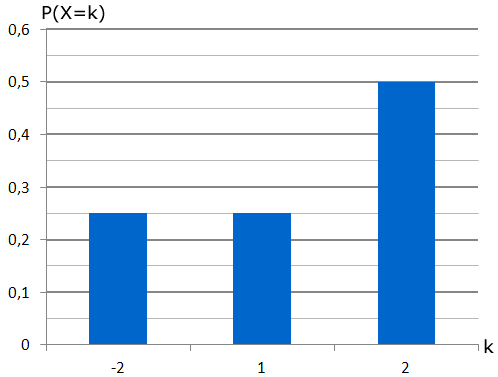
Teilaufgabe Teil A 2a (2 BE)

Ermitteln Sie mithilfe der Abbildung den Erwartungswert der Zufallsgröße

X

Teilaufgabe Teil A 2b (3 BE)

Das Zufallsexperiment wird zweimal durchgeführt. Dabei wird jeweils der Wert der Zufallsgröße

X

notiert. Bestimmen Sie die Wahrscheinlichkeit dafür, dass die Summe dieser beiden Werte negativ ist.

Die beiden Diagramme zeigen für die Bevölkerungsgruppe der über 14-Jährigen in Deutschland Daten zur Altersstruktur und zum Besitz von Mobiltelefonen.

Aus den über 14-Jährigen in Deutschland wird eine Person zufällig ausgewählt. Betrachtet werden folgende Ereignisse:

M

: "Die Person besitzt ein Mobiltelefon."

S

: "Die Person ist 65 Jahre oder älter."

E

: "Mindestens eines der Ereignisse

M

und

S

tritt ein."

Teilaufgabe Teil B 1a (2 BE)

Geben Sie an, welche zwei der folgenden Mengen I bis VI jeweils das Ereignis

E

beschreiben.

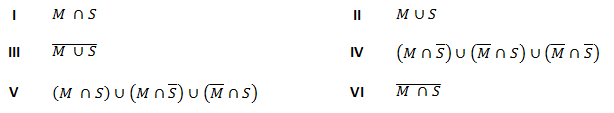
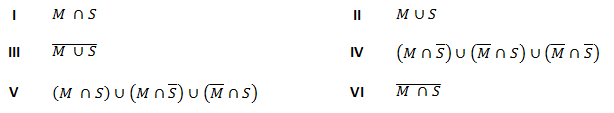
Teilaufgabe Teil B 1b (3 BE)

Entscheiden Sie anhand geeigneter Terme und auf der Grundlage der vorliegenden Daten, welche der beiden folgenden Wahrscheinlichkeiten größer ist. Begründen Sie Ihre Entscheidung.

p_{1}

ist die Wahrscheinlichkeit dafür, dass die ausgewählte Person ein Mobiltelefon besitzt, wenn bekannt ist, dass sie 65 Jahre oder älter ist.

p_{2}

ist die Wahrscheinlichkeit dafür, dass die ausgewählte Person 65 Jahre oder älter ist, wenn bekannt ist, dass sie ein Mobiltelefon besitzt.

Teilaufgabe Teil B 1c (5 BE)

Erstellen Sie zu dem beschriebenen Sachverhalt für den Fall, dass das Ereignis

E

mit einer Wahrscheinlichkeit von

98 %

eintritt, eine vollständig ausgefüllte Vierfeldertafel. Bestimmen Sie für diesen Fall die Wahrscheinlichkeit

P_{S} (M) .

Zwei Drittel der Senioren in Deutschland besitzen ein Mobiltelefon. Bei einer Talkshow zum Thema "Chancen und Risiken der digitalen Welt" sitzen 30 Senioren im Publikum.

Teilaufgabe Teil B 2a (3 BE)

Bestimmen Sie die Wahrscheinlichkeit dafür, dass unter

30

zufällig ausgewählten Senioren in Deutschland mindestens

17

und höchstens

23

ein Mobiltelefon besitzen.

Teilaufgabe Teil B 2b (3 BE)

Von den

30

Senioren im Publikum besitzen

24

ein Mobiltelefon. Im Verlauf der Sendung werden drei der Senioren aus dem Publikum zufällig ausgewählt und nach ihrer Meinung befragt. Bestimmen Sie die Wahrscheinlichkeit dafür, dass genau zwei dieser drei Senioren ein Mobiltelefon besitzen.

Teilaufgabe Teil B 3 (4 BE)

Eine Handelskette hat noch zahlreiche Smartphones des Modells

Y 3

auf Lager, als der Hersteller das Nachfolgemodell

Y 4

auf den Markt bringt. Der Einkaufspreis für das neue

Y 4

beträgt

300

€, während die Handelskette für das Vorgängermodell

Y 3

im Einkauf nur

250

€ bezahlen musste. Um die Lagerbestände noch zu verkaufen, bietet die Handelskette ab dem Verkaufsstart des

Y 4

die Smartphones des Typs

Y 3

für je

199

€ an.
Aufgrund früherer Erfahrungen geht die Handelskette davon aus, dass von den verkauften Smartphones der Modelle

Y 3

und

Y 4

trotz des Preisnachlasses nur

26 %

vom Typ

Y 3

sein werden. Berechnen Sie unter dieser Voraussetzung, zu welchem Preis die Handelskette das

Y 4

anbieten muss, damit sie voraussichtlich pro verkauftem Smartphone der Modelle

Y 3

und

Y 4

im Mittel

97

€ mehr erhält, als sie beim Einkauf dafür zahlen musste.

Alle Abituraufgaben

Lösungen zu:

Teilaufgabe Teil A 1a

Teilaufgabe Teil A 1b

Teilaufgabe Teil A 2a

Teilaufgabe Teil A 2b

Teilaufgabe Teil B 1a

Teilaufgabe Teil B 1b

Teilaufgabe Teil B 1c

Teilaufgabe Teil B 2a

Teilaufgabe Teil B 2b

Teilaufgabe Teil B 3

Lösung als Video:

Themen-Übersicht

Tipp:

Arbeite frühzeitig mit der Merkhilfe Mathematik,
die als Hilfsmittel im Abitur zugelassen ist.

Feedback:

Du hast einen Fehler gefunden oder hast Anregungen zur Internetseite?

Teile uns Dein Feedback mit!