Abitur 2020 Mathematik Stochastik III

Gegeben sind grüne und rote Würfel, deren Seitenflächen unterschiedlich beschriftet sind und beim Werfen mit jeweils gleicher Wahrscheinlichkeit auftreten. Jeder grüne Würfel trägt auf fünf Seitenflächen die Augenzahl 1 und auf einer die Augenzahl 6. Jeder rote Würfel trägt auf jeweils zwei Seitenflächen die Augenzahlen 1, 3 bzw. 6.

Teilaufgabe Teil A a (2 BE)

In einer Urne befinden sich drei grüne Würfel und zwei rote Würfel. Der Urne werden mit einem Griff zwei Würfel zufällig entnommen. Geben Sie einen Term an, mit dem man die Wahrscheinlichkeit dafür bestimmen kann, dass ein roter Würfel und ein grüner Würfel entnommen werden.

Teilaufgabe Teil A b (3 BE)

Ein grüner Würfel und ein roter Würfel werden gleichzeitig geworfen. Die Zufallsgröße

X

beschreibt die Summe der beiden geworfenen Augenzahlen. Geben Sie alle Werte an, die die Zufallsgröße

X

annehmen kann, und bestimmen Sie die Wahrscheinlichkeit

P (X = 7)

Teilaufgabe Teil B 1 (5 BE)

In einer Gemeinde gibt es 6250 Haushalte, von denen 2250 über einen schnellen Internetanschluss verfügen. Zwei Drittel der Haushalte, die über einen schnellen Internetanschluss verfügen, besitzen auch ein Abonnement eines Streamingdiensts.

46 %

aller Haushalte verfügen weder über einen schnellen Internetanschluss noch besitzen sie ein Abonnement eines Streamingdiensts.

Betrachtet werden die folgenden Ereignisse:

A :

"Ein zufällig ausgewählter Haushalt verfügt über einen schnellen Internetanschluss."

B :

"Ein zufällig ausgewählter Haushalt besitzt ein Abonnement eines Streamingdiensts."

Stellen Sie zu der beschriebenen Situation eine vollständig ausgefüllte Vierfeldertafel auf und überprüfen Sie, ob die Ereignisse

A

und

B

stochastisch unabhängig sind.

Ein Telekommunikationsunternehmen möchte neue Kunden gewinnen. Dazu schickt es an zufällig ausgewählte Haushalte Werbematerial. Im Folgenden soll davon ausgegangen werden, dass die angeschriebenen Haushalte unabhängig voneinander mit einer Wahrscheinlichkeit von jeweils

20 %

noch nicht über einen schnellen Internetanschluss verfügen.

Teilaufgabe Teil B 2a (4 BE)

Ermitteln Sie jeweils die Wahrscheinlichkeit dafür, dass unter 10 angeschriebenen Haushalten

mindestens zwei noch nicht über einen schnellen Internetanschluss verfügen.
genau acht bereits über einen schnellen Internetanschluss verfügen.

Teilaufgabe Teil B 2b (2 BE)

Beschreiben Sie im Sachzusammenhang ein Ereignis, dessen Wahrscheinlichkeit durch den Term

0, 2^{10} + (1 - 0, 2)^{10}

angegeben wird.

Teilaufgabe Teil B 2c (5 BE)

Ermitteln Sie, wie viele Haushalte das Unternehmen mindestens anschreiben müsste, damit mit einer Wahrscheinlichkeit von mehr als

99 %

wenigstens ein angeschriebener Haushalt, der noch nicht über einen schnellen Internetanschluss verfügt, einen solchen einrichten lassen würde. Gehen Sie dabei davon aus, dass sich jeder hundertste angeschriebene Haushalt, der noch nicht über einen schnellen Internetanschluss verfügt, dafür entscheidet, einen solchen einrichten zu lassen.

Die Zufallsgröße

Y

kann die Werte 0, 1, 2, 3 und 4 annehmen. Die Tabelle zeigt die Wahrscheinlichkeitsverteilung von

Y

mit

a, b \in [0; 1]

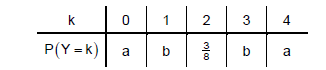
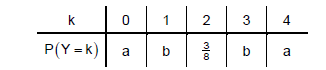
Teilaufgabe Teil B 3a (2 BE)

Beschreiben Sie, woran man unmittelbar erkennen kann, dass der Erwartungswert von

Y

gleich 2 ist.

Die Varianz von

Y

ist gleich

\frac{11}{8}

Teilaufgabe Teil B 3b (5 BE)

Bestimmen Sie die Werte von

a

und

b

Teilaufgabe Teil B 3c (2 BE)

Die Zufallsgröße

Z

, die für eine Laplace-Münze die Anzahl des Auftretens von "Zahl" bei viermaligem Werfen beschreibt, hat ebenfalls den Erwartungswert 2 und es gilt analog

P (Z = 2) = \frac{3}{8}

. Berechnen Sie die Varianz von

Z

, vergleichen Sie diese mit der Varianz von

Y

und beschreiben Sie davon ausgehend einen qualitativen Unterschied der Wahrscheinlichkeitsverteilungen von

Z

und

Y

Alle Abituraufgaben

Lösungen zu:

Teilaufgabe Teil A a

Teilaufgabe Teil A b

Teilaufgabe Teil B 1

Teilaufgabe Teil B 2a

Teilaufgabe Teil B 2b

Teilaufgabe Teil B 2c

Teilaufgabe Teil B 3a

Teilaufgabe Teil B 3b

Teilaufgabe Teil B 3c

Lösung als Video:

Themen-Übersicht

Tipp:

Arbeite frühzeitig mit der Merkhilfe Mathematik,
die als Hilfsmittel im Abitur zugelassen ist.

Feedback:

Du hast einen Fehler gefunden oder hast Anregungen zur Internetseite?

Teile uns Dein Feedback mit!