über 250 kostenlose
Abituraufgaben
Lösung als Video
und ausformuliert
Alle Lösungen von
erfahrenen Lehrern
Abitur 2018 Mathematik Stochastik III
In Sonnenstadt gibt es Einfamilienhäuser, von denen mit einer Holzpelletheizung ausgestattet sind. Bei zwei Dritteln der Einfamilienhäuser mit Holzpelletheizung ist diese mit einer solarthermischen Anlage kombiniert. aller Einfamilienhäuser sind weder mit einer Holzpelletheizung noch mit einer solarthermischen Anlage ausgestattet.
Teilaufgabe Teil A 1a (3 BE)
Stellen Sie zu der beschriebenen Situation eine vollständig ausgefüllte Vierfeldertafel auf.
Teilaufgabe Teil A 1b (2 BE)
Ein zufällig ausgewähltes Einfamilienhaus ist mit einer solarthermischen Anlage ausgestattet. Mit welcher Wahrscheinlichkeit hat es eine Holzpelletheizung?
Das abgebildete Baumdiagramm stellt ein zweistufiges Zufallsexperiment mit den Ereignissen und sowie deren Gegenereignissen und dar.
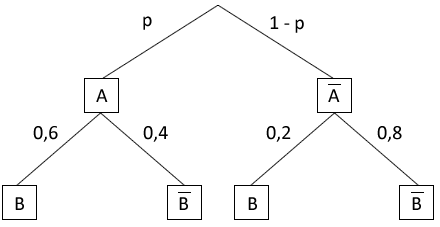

Teilaufgabe Teil A 2a (2 BE)
Bestimmen Sie den Wert von so, dass das Ereignis bei diesem Zufallsexperiment mit der Wahrscheinlichkeit eintritt.
Teilaufgabe Teil A 2b (3 BE)
Ermitteln Sie den größtmöglichen Wert, den die Wahrscheinlichkeit von annehmen kann.
Auf einem Abschnitt einer wenig befahrenen Landstraße ist eine Höchstgeschwindigkeit von 80 km/h zugelassen. An einer Stelle dieses Abschnitts wird die Geschwindigkeit vorbeifahrender Pkw gemessen. Im Folgenden werden vereinfachend nur solche Fahrten betrachtet, bei denen die Fahrer die Geschwindigkeit unabhängig voneinander wählen konnten.
Für die ersten 200 erfassten Fahrten ergab sich nach Einteilung in Geschwindigkeitsklassen die folgende Verteilung:
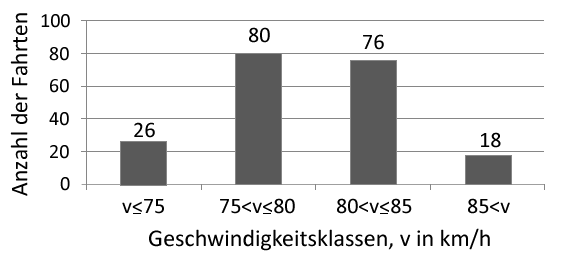
Bei der Fahrten war der Fahrer allein unterwegs, dieser Alleinfahrer fuhren zu schnell. Aus den Fahrten wird eine zufällig ausgewählt.
Es werden folgende Ereignisse betrachtet:
: "Der Fahrer war allein unterwegs."
: "Der Pkw war zu schnell."

Bei der Fahrten war der Fahrer allein unterwegs, dieser Alleinfahrer fuhren zu schnell. Aus den Fahrten wird eine zufällig ausgewählt.
Es werden folgende Ereignisse betrachtet:
: "Der Fahrer war allein unterwegs."
: "Der Pkw war zu schnell."
Teilaufgabe Teil B 1a (5 BE)
Weisen Sie nach, dass die Ereignisse und stochastisch abhängig sind, und geben Sie hierfür einen möglichen Grund im Sachzusammenhang an.
Die Geschwindigkeitsmessungen werden über einen längeren Zeitraum fortgesetzt. Dabei zeigt sich, dass die Verteilung der auf km/h genau gemessenen Geschwindigkeiten näherungsweise durch eine Binomialverteilung mit den Parametern und beschrieben werden kann. Beispielsweise entspricht näherungsweise dem Anteil der mit einer Geschwindigkeit von 77 km/h erfassten Pkw.
Teilaufgabe Teil B 1b (4 BE)
Bestätigen Sie exemplarisch für eine der beiden mittleren Geschwindigkeitsklassen der oben dargestellten Stichprobe, dass die ermittelte Anzahl der Fahrten mit der Beschreibung durch die Binomialverteilung im Einklang steht.
Teilaufgabe Teil B 1c (2 BE)
Bestimmen Sie unter Verwendung dieser Binomialverteilung die kleinste Geschwindigkeit , für die die folgende Aussage zutrifft: "Bei mehr als der erfassten Fahrten wird nicht überschritten."
Die Polizei führt an der Messstelle eine Geschwindigkeitskontrolle durch.
Bei einer Geschwindigkeit von mehr als 83 km/h liegt ein Tempoverstoß vor.
Vereinfachend soll davon ausgegangen werden, dass die Geschwindigkeit eines vorbeifahrenden Pkw mit einer Wahrscheinlichkeit von größer als 83 km/h ist.
Bei einer Geschwindigkeit von mehr als 83 km/h liegt ein Tempoverstoß vor.
Vereinfachend soll davon ausgegangen werden, dass die Geschwindigkeit eines vorbeifahrenden Pkw mit einer Wahrscheinlichkeit von größer als 83 km/h ist.
Teilaufgabe Teil B 2a (4 BE)
Berechnen Sie die Anzahl der Geschwindigkeitsmessungen, die mindestens durchgeführt werden müssen, damit mit einer Wahrscheinlichkeit von mehr als mindestens ein Tempoverstoß erfasst wird.
Teilaufgabe Teil B 2b (5 BE)
Liegt in einer Stichprobe von 50 Geschwindigkeitsmessungen die Zahl der Tempoverstöße um mehr als eine Standardabweichung unter dem Erwartungswert, geht die Polizei davon aus, dass wirksam vor der Geschwindigkeitskontrolle gewarnt wurde, und bricht die Kontrolle ab. Bestimmen Sie die Wahrscheinlichkeit dafür, dass die Geschwindigkeitskontrolle fortgeführt wird, obwohl die Wahrscheinlichkeit dafür, dass ein Tempoverstoß begangen wird, auf gesunken ist.
Lösungen zu:
Tipp:
Arbeite frühzeitig mit der Merkhilfe Mathematik,
die als Hilfsmittel im Abitur zugelassen ist.
die als Hilfsmittel im Abitur zugelassen ist.
Feedback:
Du hast einen Fehler gefunden oder hast Anregungen zur Internetseite?








