Abitur 2017 Mathematik Stochastik III

Ein Glücksrad hat drei Sektoren, einen blauen, einen gelben und einen roten. Diese sind unterschiedlich groß. Die Wahrscheinlichkeit dafür, dass beim einmaligen Drehen der blaue Sektor getroffen wird, beträgt

p

Teilaufgabe Teil A 1a (2 BE)

Interpretieren Sie den Term

(1 - p)^{7}

im Sachzusammenhang.

Teilaufgabe Teil A 1b (1 BE)

Das Glücksrad wird zehnmal gedreht. Geben Sie einen Term an, mit dem die Wahrscheinlichkeit dafür berechnet werden kann, dass der blaue Sektor genau zweimal getroffen wird.

Teilaufgabe Teil A 1c (2 BE)

Die Wahrscheinlichkeit dafür, dass beim einmaligen Drehen der gelbe Sektor getroffen wird, beträgt 50%. Felix hat 100 Drehungen des Glücksrads beobachtet und festgestellt, dass bei diesen der Anteil der Drehungen, bei denen der gelbe Sektor getroffen wurde, deutlich geringer als 50% war. Er folgert: "Der Anteil der Drehungen, bei denen der gelbe Sektor getroffen wird, muss also bei den nächsten 100 Drehungen deutlich größer als 50% sein." Beurteilen Sie die Aussage von Felix.

Teilaufgabe Teil A 1d (2 BE)

Das Glücksrad wird viermal gedreht und die Abfolge der Farben als Ergebnis notiert. Bestimmen Sie die Anzahl der möglichen Ergebnisse, in denen die Farbe Blau nicht vorkommt.

Teilaufgabe Teil A 2 (3 BE)

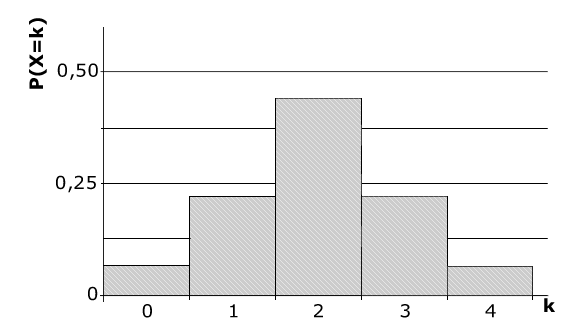
In der Abbildung ist die Wahrscheinlichkeitsverteilung einer Zufallsgröße

X

mit der Wertemenge

{0; 1; 2; 3; 4}

und dem Erwartungswert 2 dargestellt. Weisen Sie nach, dass es sich dabei nicht um eine Binomialverteilung handeln kann.

Das elektronische Stabilitätsprogramm (ESP) eines Autos kann Schleuderbewegungen und damit Unfälle verhindern.

Gehen Sie bei den folgenden Aufgaben davon aus, dass 40% aller Autos mit ESP ausgerüstet sind.

200 Autos werden nacheinander zufällig ausgewählt; die Zufallsgröße

X

beschreibt die Anzahl der ausgewählten Autos mit ESP.

Teilaufgabe Teil B 1a (3 BE)

Bestimmen Sie die Wahrscheinlichkeit dafür, dass von den ausgewählten Autos mindestens 70 mit ESP ausgerüstet sind.

Teilaufgabe Teil B 1b (7 BE)

Bestimmen Sie die Wahrscheinlichkeiten folgender Ereignisse.

A

: "Das fünfte ausgewählte Auto ist das erste mit ESP."

B

: "Die Zufallsgröße

X

nimmt einen Wert an, der von ihrem Erwartungswert höchstens um eine Standardabweichung abweicht."

In einem Parkhaus befinden sich insgesamt 100 Parkplätze.

Teilaufgabe Teil B 2a (3 BE)

Im Parkhaus sind 20 Parkplätze frei; vier Autofahrer suchen jeweils einen Parkplatz. Formulieren Sie in diesem Sachzusammenhang zu den folgenden Termen jeweils eine Aufgabenstellung, deren Lösung sich durch den Term berechnen lässt.

$α)$

20 \cdot 19 \cdot 18 \cdot 17

$β)$

(\binom{20}{4})

Das Parkhaus ist nun mit 100 Autos besetzt, von denen 40 mit ESP ausgerüstet sind.

Teilaufgabe Teil B 2b (3 BE)

Sieben von diesen 100 Autos sind Kleinwagen und nicht mit ESP ausgerüstet, 90 sind keine Kleinwagen. Betrachtet werden folgende Ereignisse.

E

: "Ein im Parkhaus zufällig ausgewähltes Auto ist mit ESP ausgerüstet."

K

: "Bei einem im Parkhaus zufällig ausgewählten Auto handelt es sich um einen Kleinwagen."

Geben Sie die Bedeutung von

P_{K} (E)

im Sachzusammenhang an und ermitteln Sie diese Wahrscheinlichkeit.

Teilaufgabe Teil B 2c (4 BE)

30 der im Parkhaus stehenden Autos werden zufällig ausgewählt. Bestimmen Sie die Wahrscheinlichkeit dafür, dass darunter genau 40% mit ESP ausgerüstet sind.

Alle Abituraufgaben

Lösungen zu:

Teilaufgabe Teil A 1a

Teilaufgabe Teil A 1b

Teilaufgabe Teil A 1c

Teilaufgabe Teil A 1d

Teilaufgabe Teil A 2

Teilaufgabe Teil B 1a

Teilaufgabe Teil B 1b

Teilaufgabe Teil B 2a

Teilaufgabe Teil B 2b

Teilaufgabe Teil B 2c

Lösung als Video:

Themen-Übersicht

Tipp:

Arbeite frühzeitig mit der Merkhilfe Mathematik,
die als Hilfsmittel im Abitur zugelassen ist.

Feedback:

Du hast einen Fehler gefunden oder hast Anregungen zur Internetseite?

Teile uns Dein Feedback mit!