über 250 kostenlose
Abituraufgaben
Lösung als Video
und ausformuliert
Alle Lösungen von
erfahrenen Lehrern
Abitur 2015 Mathematik Stochastik III
Bei der Wintersportart Biathlon wird bei jeder Schießeinlage auf fünf Scheiben geschossen. Ein Biathlet tritt bei einem Einzelrennen zu einer Schießeinlage an, bei der er auf jede Scheibe einen Schuss abgibt. Diese Schießeinlage wird modellhaft durch eine Bernoulikette mit der Länge und der Trefferwahrscheinlichkeit beschrieben.
Teilaufgabe Teil A 1a (3 BE)
Geben Sie für die folgenden Ereignisse und jeweils einen Term an, der die Wahrscheinlichkeit des Ereignisses in Abhängigkeit von beschreibt.
A: "Der Biathlet trifft bei genau vier Schüssen."
B: "Der Biathlet trifft nur bei den ersten beiden Schüssen."
A: "Der Biathlet trifft bei genau vier Schüssen."
B: "Der Biathlet trifft nur bei den ersten beiden Schüssen."
Teilaufgabe Teil A 1b (2 BE)
Erläutern Sie anhand eines Beispiels, dass die modellhafte Beschreibung der Schießeinlage durch eine Bernoullikette unter Umständen der Realität nicht gerecht wird.
Ein Moderator lädt zu einer Talkshow drei Politiker, eine Journalistin und zwei Mitglieder einer Bürgerinitiative ein. Für die Diskussionsrunde ist eine halbkreisförmige Sitzordnung vorgesehen, bei der nach den Personen unterschieden wird und der Moderator den mittleren einnimmt.
Teilaufgabe Teil A 2a (1 BE)
Geben Sie einen Term an, mit dem die Anzahl der möglichen Sitzordnungen berechnet werden kann, wenn keine weiteren Einschränkungen berücksichtigt werden.
Teilaufgabe Teil A 2b (4 BE)
Der Sender hat festgelegt, dass unmittelbar neben dem Moderator auf einer Seite die Journalistin und auf der anderen Seite einer der Politiker sitzen soll. Berechnen Sie unter Berücksichtigung dieser weiteren Einschränkung die Anzahl der möglichen Sitzordnungen.
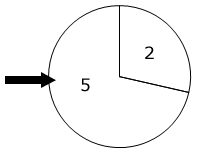
Der Marketingchef einer Handelskette plant eine Werbeaktion, bei der ein Kunde die Höhe des Rabatts bei seinem Einkauf durch zweimaliges Drehen an einem Glücksrad selbst bestimmen kann. Das Glücksrad hat zwei Sektoren, die mit den Zahlen bzw. beschriftet sind (vgl. Abbildung).
Der Rabatt in Prozent errechnet sich als Produkt der beiden Zahlen, die der Kunde bei zweimaligem Drehen am Glücksrad erzielt.
Die Zufallsgröße beschreibt die Höhe dieses Rabatts in Prozent, kann also die Werte , oder annehmen. Die Zahl wird beim Drehen des Glücksrads mit der Wahrscheinlichkeit erzielt.
Vereinfachend soll davon ausgegangen werden, dass jeder Kunde genau einen Einkauf tätigt und auch tatsächlich am Glücksrad dreht.
Der Rabatt in Prozent errechnet sich als Produkt der beiden Zahlen, die der Kunde bei zweimaligem Drehen am Glücksrad erzielt.
Die Zufallsgröße beschreibt die Höhe dieses Rabatts in Prozent, kann also die Werte , oder annehmen. Die Zahl wird beim Drehen des Glücksrads mit der Wahrscheinlichkeit erzielt.
Vereinfachend soll davon ausgegangen werden, dass jeder Kunde genau einen Einkauf tätigt und auch tatsächlich am Glücksrad dreht.

Teilaufgabe Teil B 1a (3 BE)
Ermitteln Sie mithilfe eines Baumdiagramms die Wahrscheinlichkeit dafür, dass ein Kunde bei seinem Einkauf einen Rabatt von erhält.
(Ergebnis: )
(Ergebnis: )
Teilaufgabe Teil B 1b (3 BE)
Zeigen Sie, dass für den Erwartungswert der Zufallsgröße gilt:
Teilaufgabe Teil B 1c (3 BE)
Die Geschäftsführung will im Mittel für einen Einkauf einen Rabatt von gewähren. Berechnen Sie für diese Vorgabe den Wert der Wahrscheinlichkeit .
Teilaufgabe Teil B 1d (4 BE)
Die Wahrscheinlichkeit, dass ein Kunde bei seinem Einkauf den niedrigsten Rabatt erhält, beträgt . Bestimmen Sie, wie viele Kunden mindestens an dem Glücksrad drehen müssen, damit mit einer Wahrscheinlichkeit von mehr als mindestens einer der Kunden den niedrigsten Rabatt erhält.
Eine der Filialen der Handelskette befindet sich in einem Einkaufszentrum, das zu Werbezwecken die Erstellung einer Smartphone-App in Auftrag geben will. Diese App soll die Kunden beim Betreten des Einkaufszentrums über aktuelle Angebote und Rabattaktionen der beteiligten Geschäfte informieren. Da dies mit Kosten verbunden ist, will der Finanzchef der Handelskette einer Beteiligung an der App nur zustimmen, wenn mindestens der Kunden der Filiale bereit sind, diese App zu nutzen. Der Marketingchef warnt jedoch davor, auf eine Beteiligung an der App zu verzichten, da dies zu einem Imageverlust führen könnte.
Um zu einer Entscheidung zu gelangen, will die Geschäftsführung der Handelskette eine der beiden folgenden Nullhypothesen auf der Basis einer Befragung von Kunden auf einem Signifikanzniveau von testen:
I "Weniger als der Kunden sind bereit, die App zu nutzen."
II "Mindestens der Kunden sind bereit, die App zu nutzen."
Um zu einer Entscheidung zu gelangen, will die Geschäftsführung der Handelskette eine der beiden folgenden Nullhypothesen auf der Basis einer Befragung von Kunden auf einem Signifikanzniveau von testen:
I "Weniger als der Kunden sind bereit, die App zu nutzen."
II "Mindestens der Kunden sind bereit, die App zu nutzen."
Teilaufgabe Teil B 2a (4 BE)
Nach Abwägung der möglichen Folgen, die der Finanzchef und der Marketingchef aufgezeigt haben, wählt die Geschäftsführung für den Test die Nullhypothese II. Bestimmen Sie die zugehörige Entscheidungsregel.
Teilaufgabe Teil B 2b (3 BE)
Entscheiden Sie, ob bei der Abwägung, die zur Wahl der Nullhypothese II führte, die Befürchtung eines Imageverlusts oder die Kostenfrage als schwerwiegender erachtet wurde. Erläutern Sie Ihre Entscheidung.
Lösungen zu:
Tipp:
Arbeite frühzeitig mit der Merkhilfe Mathematik,
die als Hilfsmittel im Abitur zugelassen ist.
die als Hilfsmittel im Abitur zugelassen ist.
Feedback:
Du hast einen Fehler gefunden oder hast Anregungen zur Internetseite?








