über 250 kostenlose
Abituraufgaben
Lösung als Video
und ausformuliert
Alle Lösungen von
erfahrenen Lehrern
Toggle navigation
Lösungen zu:
Lösung als Video:
Themen-Übersicht
Tipp:
Arbeite frühzeitig mit der Merkhilfe Mathematik,
die als Hilfsmittel im Abitur zugelassen ist.
Feedback:
Du hast einen
Fehler
gefunden oder hast Anregungen zur Internetseite?
Abitur 2015 Mathematik Analytische Geometrie VI
Lösungen zu:
Lösung als Video:
Themen-Übersicht
Tipp:
Arbeite frühzeitig mit der Merkhilfe Mathematik,
die als Hilfsmittel im Abitur zugelassen ist.
die als Hilfsmittel im Abitur zugelassen ist.
Feedback:
Du hast einen Fehler gefunden oder hast Anregungen zur Internetseite?
Die Gerade verläuft durch die Punkte und .
Teilaufgabe Teil A 1a (3 BE)
Zeigen Sie, dass die Punkte und den Abstand haben.
Die Punkte und liegen auf und haben von jeweils den Abstand . Bestimmen Sie die Koordinaten von und .
Die Punkte und liegen auf und haben von jeweils den Abstand . Bestimmen Sie die Koordinaten von und .
Teilaufgabe Teil A 1b (2 BE)
Die Punkte und sollen mit einem weiteren Punkt die Eckpunkte eines Parallelogramms bilden. Für die Lage des vierten Eckpunkts gibt es mehrere Möglichkeiten.
Geben Sie für zwei dieser Möglichkeiten die Koordinaten des vierten Eckpunkts an.
Geben Sie für zwei dieser Möglichkeiten die Koordinaten des vierten Eckpunkts an.
Die Abbildung zeigt die Pyramide mit quadratischer Grundfläche . Der Pyramide ist eine Stufenpyramide einbeschrieben, die aus Würfeln mit der Kantenlänge besteht.
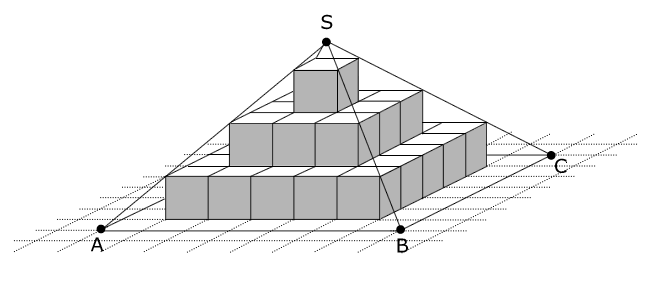
Teilaufgabe Teil A 2a (2 BE)
Geben Sie das Volumen der Stufenpyramide und die Höhe der Pyramide an.
Teilaufgabe Teil A 2b (3 BE)
Bestimmen Sie unter Verwendung eines geeignet gewählten kartesischen Koordinatensystems eine Gleichung für die Gerade, die durch die Punkte und verläuft.
Zeichnen Sie das gewählte Koordinatensystem in die Abbildung ein.
Zeichnen Sie das gewählte Koordinatensystem in die Abbildung ein.
| Abbildung 1 zeigt eine Sonnenuhr mit einer gegenüber der Horizontalen geneigten, rechteckigen Grundplatte, auf der sich ein kreisförmiges Zifferblatt befindet. Auf der Grundplatte ist der Polstab befestigt, dessen Schatten bei Sonneneinstrahlung die Uhrzeit auf dem Zifferblatt anzeigt. Eine Sonnenuhr dieser Bauart wird in einem kartesischen Koordinatensystem modellhaft dargestellt (vgl. Abbildung 2). Dabei beschreibt das Rechteck mit und die Grundplatte der Sonnenuhr. Der Befestigungspunkt des Polstabs auf der Grundplatte wird im Modell durch den Diagonalenschnittpunkt des Rechtecks dargestellt. Eine Längeneinheit im Koordinatensystem entspricht cm in der Realität. Die Horizontale wird im Modell durch die -Ebene beschrieben. |   |
Teilaufgabe Teil B a (5 BE)
Bestimmen Sie die Koordinaten des Punkts . Ermitteln Sie eine Gleichung der Ebene , in der das Rechteck liegt, in Normalenform.
(mögliches Teilergebnis: )
(mögliches Teilergebnis: )
Teilaufgabe Teil B b (4 BE)
Die Grundplatte ist gegenüber der Horizontalen um den Winkel geneigt. Damit man mit der Sonnenuhr die Uhrzeit korrekt bestimmen kann, muss für den Breitengrad des Aufstellungsorts der Sonnenuhr gelten. Bestimmen Sie, für welchen Breitengrad die Sonnenuhr gebaut wurde.
Teilaufgabe Teil B c (3 BE)
Der Polstab wird im Modell durch die Strecke mit dargestellt. Zeigen Sie, dass der Polstab senkrecht auf der Grundplatte steht, und berechnen Sie die Länge des Polstabs auf Zentimeter genau.
Sonnenlicht, das an einem Sommertag zu einem bestimmten Zeitpunkt auf die Sonnenuhr einfällt, wird im Modell durch parallele Geraden mit dem Richtungsvektor dargestellt.
Teilaufgabe Teil B d (6 BE)
Weisen Sie nach, dass der Schatten der im Modell durch den Punkt dargestellten Spitze des Polstabs außerhalb der rechteckigen Grundplatte liegt.
Teilaufgabe Teil B e (2 BE)
Um 6 Uhr verläuft der Schatten des Polstabs im Modell durch den Mittelpunkt der Kante , um 12 Uhr durch den Mittelpunkt der Kante und um 18 Uhr durch den Mittelpunkt der Kante Begründen Sie, dass der betrachtete Zeitpunkt vor 12 Uhr liegt.
Lösungen zu:
Lösung als Video:
Themen-Übersicht
Tipp:
Arbeite frühzeitig mit der Merkhilfe Mathematik,
die als Hilfsmittel im Abitur zugelassen ist.
die als Hilfsmittel im Abitur zugelassen ist.
Feedback:
Du hast einen Fehler gefunden oder hast Anregungen zur Internetseite?
© 2001 - 2025 Abiturloesung.de. Alle Rechte vorbehalten.
