über 250 kostenlose
Abituraufgaben
Lösung als Video
und ausformuliert
Alle Lösungen von
erfahrenen Lehrern
Abitur 2020 Mathematik Infinitesimalrechnung II
Gegeben ist die Funktion mit maximalem Definitionsbereich .
Teilaufgabe Teil A 1a (3 BE)
Skizzieren Sie die Parabel mit der Gleichung in einem Koordinatensystem und geben Sie an.
Teilaufgabe Teil A 1b (2 BE)
Ermitteln Sie den Term der Ableitungsfunktion von .
| Die Abbildung 1 zeigt einen Teil des Graphen einer in definierten gebrochenrationalen Funktion . Die Funktion hat bei eine Polstelle ohne Vorzeichenwechsel; zudem besitzt die Gerade mit der Gleichung als schräge Asymptote. | 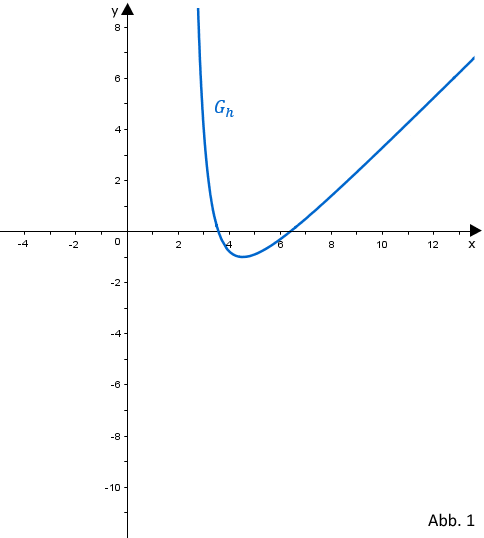 |
Teilaufgabe Teil A 2a (3 BE)
Zeichnen Sie in die Abbildung 1 die Asymptoten von ein und skizzieren Sie im Bereich einen möglichen Verlauf von .
Teilaufgabe Teil A 2b (2 BE)
Berechnen Sie unter Berücksichtigung des asymptotischen Verhaltens von einen Näherungswert für .
Gegeben ist die in definierte Funktion . Ihr Graph wird mit bezeichnet.
Teilaufgabe Teil A 3a (3 BE)
Geben Sie die Nullstellen von an und begründen Sie anhand des Funktionsterms, dass die Gerade mit der Gleichung als waagrechte Asymptote besitzt.
Teilaufgabe Teil A 3b (2 BE)
Berechnen Sie die x-Koordinate des Schnittpunkts von mit der waagrechten Asymptote.
Teilaufgabe Teil A 4 (5 BE)
Die Abbildung 2 zeigt den Graphen einer in definierten Funktion .
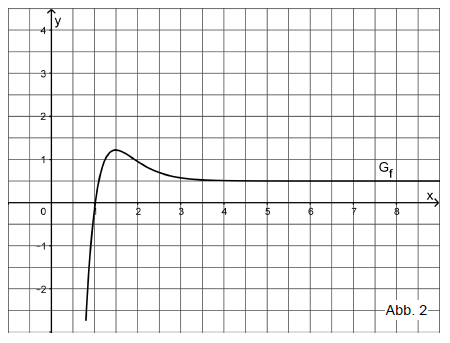
Betrachtet wird zudem die in definierte Integralfunktion .
Begründen Sie mithilfe von Abbildung 2, dass gilt, und geben Sie einen Näherungswert für den Funktionswert an. Skizzieren Sie den Graphen von in der Abbildung 2.

Betrachtet wird zudem die in definierte Integralfunktion .
Begründen Sie mithilfe von Abbildung 2, dass gilt, und geben Sie einen Näherungswert für den Funktionswert an. Skizzieren Sie den Graphen von in der Abbildung 2.
Gegeben ist die Funktion mit Definitionsbereich ; die Abbildung 1 (Teil B) zeigt ihren Graphen .
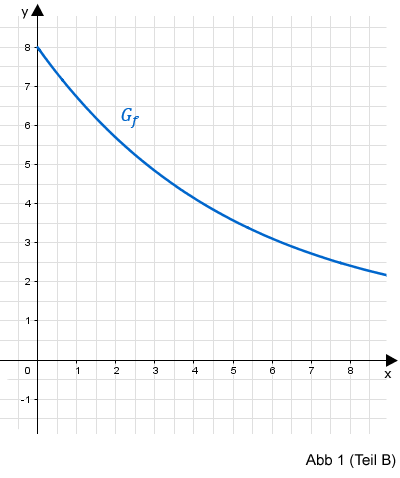

Teilaufgabe Teil B 1a (3 BE)
Begründen Sie, dass die Gerade mit der Gleichung waagrechte Asymptote von ist. Zeigen Sie rechnerisch, dass streng monoton abnehmend ist.
Für jeden Wert legen die Punkte , , und ein Rechteck mit dem Flächeninhalt fest.
Teilaufgabe Teil B 1b (7 BE)
Zeichnen Sie dieses Rechteck für in die Abbildung 1 (Teil B) ein.
Zeigen Sie, dass für einen bestimmten Wert von maximal ist, und geben Sie diesen Wert von an.
(zur Kontrolle: )
Zeigen Sie, dass für einen bestimmten Wert von maximal ist, und geben Sie diesen Wert von an.
(zur Kontrolle: )
Teilaufgabe Teil B 1c (7 BE)
Berechnen Sie den Inhalt des Flächenstücks, das von , der y-Achse sowie den Geraden mit den Gleichungen und begrenzt wird.
Einen Teil dieses Flächenstücks nimmt das zu gehörige Rechteck ein. Bestimmen Sie den prozentualen Anteil des Flächeninhalts dieses Rechtecks am Inhalt des Flächenstücks.
Einen Teil dieses Flächenstücks nimmt das zu gehörige Rechteck ein. Bestimmen Sie den prozentualen Anteil des Flächeninhalts dieses Rechtecks am Inhalt des Flächenstücks.
Die in definierte Funktion beschreibt modellhaft die zeitliche Entwicklung des Flächeninhalts eines Algenteppichs am Südufer eines Sees. Dabei ist die seit Beobachtungsbeginn vergangene Zeit in Tagen und der Flächeninhalt in Quadratmetern.
Teilaufgabe Teil B 2a (5 BE)
Bestimmen Sie sowie und geben Sie jeweils die Bedeutung des Ergebnisses im Sachzusammenhang an. Begründen Sie mithilfe des Monotonieverhaltens der Funktion , dass der Flächeninhalt des Algenteppichs im Laufe der Zeit ständig zunimmt.
Teilaufgabe Teil B 2b (4 BE)
Bestimmen Sie denjenigen Wert , für den gilt, und interpretieren Sie Ihr Ergebnis im Sachzusammenhang.
(zur Kontrolle: )
(zur Kontrolle: )
Teilaufgabe Teil B 2c (4 BE)
Bestimmen Sie die momentane Änderungsrate des Flächeninhalts des Algenteppichs zu Beobachtungsbeginn.
Teilaufgabe Teil B 2d (2 BE)
Nur zu dem Zeitpunkt, der im Modell durch (vgl. Aufgabe 2b) beschrieben wird, nimmt die momentane Änderungsrate des Flächeninhalts des Algenteppichs ihren größten Wert an. Geben Sie eine besondere Eigenschaft des Graphen von im Punkt an, die sich daraus folgern lässt, und begründen Sie Ihre Angabe.
Teilaufgabe Teil B 2e (3 BE)
Skizzieren Sie den Graphen der Funktion unter Verwendung der bisherigen Ergebnisse in der Abbildung 2 (Teil B).
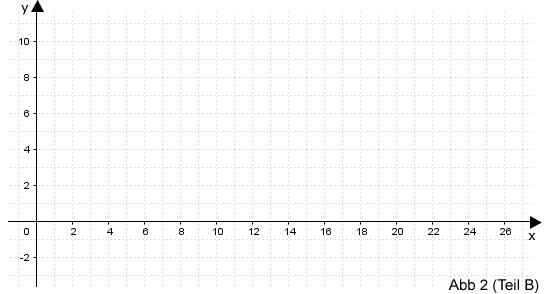

Teilaufgabe Teil B 2f (5 BE)
Um die zeitliche Entwicklung des Flächeninhalts eines Algenteppichs am Nordufer des Sees zu beschreiben, wird im Term die im Exponenten zur Basis enthaltene Zahl durch eine kleinere Zahl ersetzt.
Vergleichen Sie den Algenteppich am Nordufer mit dem am Südufer
Vergleichen Sie den Algenteppich am Nordufer mit dem am Südufer
- hinsichtlich der durch und beschriebenen Eigenschaften (vgl. Aufgabe 2a).
- hinsichtlich der momentanen Änderungsrate des Flächeninhalts zu Beobachtungsbeginn (vgl. Aufgabe 2c).
Lösungen zu:
Tipp:
Arbeite frühzeitig mit der Merkhilfe Mathematik,
die als Hilfsmittel im Abitur zugelassen ist.
die als Hilfsmittel im Abitur zugelassen ist.
Feedback:
Du hast einen Fehler gefunden oder hast Anregungen zur Internetseite?








