Abitur 2019 Mathematik Stochastik IV

Ein Glücksrad besteht aus fünf gleich großen Sektoren. Einer der Sektoren ist mit "0" beschriftet, einer mit "1" und einer mit "2"; die beiden anderen Sektoren sind mit "9" beschriftet.

Teilaufgabe Teil A 1a (2 BE)

Das Glücksrad wird viermal gedreht. Berechnen Sie die Wahrscheinlichkeit dafür, dass die Zahlen 2, 0, 1 und 9 in der angegebenen Reihenfolge erzielt werden.

Teilaufgabe Teil A 1b (3 BE)

Das Glücksrad wird zweimal gedreht. Bestimmen Sie die Wahrscheinlichkeit dafür, dass die Summe der erzielten Zahlen mindestens 11 beträgt.

Teilaufgabe Teil A 2 (2 BE)

Gegeben ist eine binomialverteilte Zufallsgröße

X

mit dem Parameterwert

n = 5

. Dem Diagramm in Abbildung 1 kann man die Wahrscheinlichkeitswerte

P (X \leq k)

mit

k \in {0; 1; 2; 3; 4}

entnehmen.
Ergänzen Sie den zu

k = 5

gehörenden Wahrscheinlichkeitswert im Diagramm. Ermitteln Sie näherungsweise die Wahrscheinlichkeit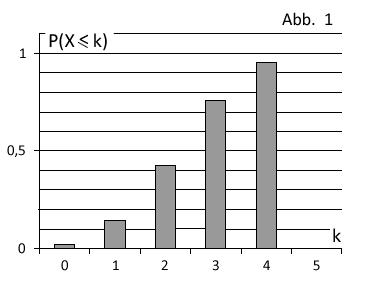

P (X = 2)

Teilaufgabe Teil A 3 (3 BE)

Das Baumdiagramm in Abbildung 2 gehört zu einem Zufallsexperiment mit den stochastisch unabhängigen Ereignissen A und B. Bestimmen Sie die Wahrscheinlichkeit des Ereignisses B.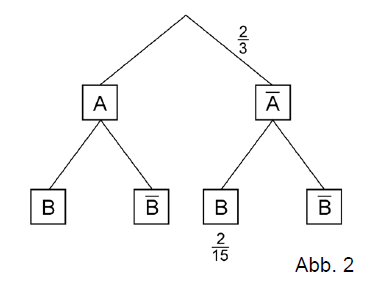

Jeder sechste Besucher eines Volksfests trägt ein Lebkuchenherz um den Hals. Während der Dauer des Volksfests wird 25-mal ein Besucher zufällig ausgewählt. Die Zufallsgröße

X

beschreibt die Anzahl der ausgewählten Besucher, die ein Lebkuchenherz tragen.

Teilaufgabe Teil B 1a (2 BE)

Bestimmen Sie die Wahrscheinlichkeit dafür, dass unter den ausgewählten Besuchern höchstens ein Besucher ein Lebkuchenherz trägt.

Teilaufgabe Teil B 1b (2 BE)

Beschreiben Sie im Sachzusammenhang ein Ereignis, dessen Wahrscheinlichkeit mit dem Term

\sum_{i = 5}^{8} (25; \frac{1}{6}; i)

berechnet werden kann.

Teilaufgabe Teil B 1c (4 BE)

Bestimmen Sie die Wahrscheinlichkeit dafür, dass der Wert der Zufallsgröße

X

höchstens um eine Standardabweichung vom Erwartungswert der Zufallsgröße abweicht.

Teilaufgabe Teil B 2 (5 BE)

Bei einer Losbude wird damit geworben, dass jedes Los gewinnt. Die Lose und die zugehörigen Sachpreise können drei Kategorien zugeordnet werden, die mit "Donau", "Main" und "Lech" bezeichnet werden. Im Lostopf befinden sich viermal so viele Lose der Kategorie "Main" wie Lose der Kategorie "Donau". Ein Los kostet 1 Euro. Die Inhaberin der Losbude bezahlt im Einkauf für einen Sachpreis in der Kategorie "Donau" 8 Euro, in der Kategorie "Main" 2 Euro und in der Kategorie "Lech" 20 Cent. Ermitteln Sie, wie groß der Anteil der Lose der Kategorie "Donau" sein muss, wenn die Inhaberin im Mittel einen Gewinn von 35 Cent pro Los erzielen will.

Die Inhaberin der Losbude beschäftigt einen Angestellten, der Besucher des Volksfests anspricht, um diese zum Kauf von Losen zu animieren. Sie ist mit der Erfolgsquote des Angestellten unzufrieden.

Teilaufgabe Teil B 3a (5 BE)

Die Inhaberin möchte dem Angestellten das Gehalt kürzen, wenn weniger als

15 %

der angesprochenen Besucher Lose kaufen. Die Entscheidung über die Gehaltskürzung soll mithilfe eines Signifikanztests auf der Grundlage von 100 angesprochenen Besuchern getroffen werden. Dabei soll möglichst vermieden werden, dem Angestellten das Gehalt zu Unrecht zu kürzen. Geben Sie die entsprechende Nullhypothese an und ermitteln Sie die zugehörige Entscheidungsregel auf dem Signifikanzniveau von

10 %

Teilaufgabe Teil B 3b (2 BE)

Der Angestellte konnte bei der Durchführung des Tests zehn von 100 erwachsenen Besuchern dazu animieren, Lose zu kaufen. Er behauptet, dass er zumindest bei Personen mit Kind eine Erfolgsquote größer als

10 %

habe. Unter den 100 angesprochenen Besuchern befanden sich 40 Personen mit Kind. Von den Personen ohne Kind zogen 54 kein Los. Überprüfen Sie, ob das Ergebnis der Stichprobe die Behauptung des Angestellten stützt.

Alle Abituraufgaben

Lösungen zu:

Teilaufgabe Teil A 1a

Teilaufgabe Teil A 1b

Teilaufgabe Teil A 2

Teilaufgabe Teil A 3

Teilaufgabe Teil B 1a

Teilaufgabe Teil B 1b

Teilaufgabe Teil B 1c

Teilaufgabe Teil B 2

Teilaufgabe Teil B 3a

Teilaufgabe Teil B 3b

Lösung als Video:

Themen-Übersicht

Tipp:

Arbeite frühzeitig mit der Merkhilfe Mathematik,
die als Hilfsmittel im Abitur zugelassen ist.

Feedback:

Du hast einen Fehler gefunden oder hast Anregungen zur Internetseite?

Teile uns Dein Feedback mit!