Abitur 2020 Mathematik Infinitesimalrechnung I

Gegeben ist die Funktion

h : x \mapsto x \cdot \ln (x^{2})

mit maximalem Definitionsbereich

D_{h}

Teilaufgabe Teil A 1a (2 BE)

Geben Sie

D_{h}

an und zeigen Sie, dass für den Term der Ableitungsfunktion

h^{'}

von

h

gilt:

h^{'} (x) = \ln (x^{2}) + 2

Teilaufgabe Teil A 1b (3 BE)

Bestimmen Sie die Koordinaten des im II. Quadranten liegenden Hochpunkts des Graphen von

h

Die Abbildung 1 zeigt den Graphen

G_{f^{'}}

der Ableitungsfunktion

f^{'}

einer in

ℝ

definierten ganzrationalen Funktion

f

. Nur in den Punkten

(- 4 | f^{'} (- 4))

und

(5 | f^{'} (5))

hat der Graph

G_{f^{'}}

waagrechte Tangenten.

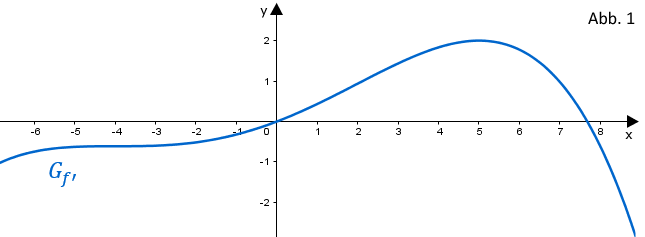
Teilaufgabe Teil A 2a (2 BE)

Begründen Sie, dass

f

genau eine Wendestelle besitzt.

Teilaufgabe Teil A 2b (2 BE)

Es gibt Tangenten an den Graphen von

f

, die parallel zur Winkelhalbierenden des I. und III. Quadranten sind. Ermitteln Sie anhand des Graphen

G_{f^{'}}

der Ableitungsfunktion

f^{'}

in der Abbildung 1 Näherungswerte für die

x

-Koordinaten derjenigen Punkte, in denen der Graph von

f

jeweils eine solche Tangente hat.

Gegeben sind die in

ℝ

definierten Funktionen

f : x \mapsto x^{2} + 4

und

g_{m} : x \mapsto m \cdot x

mit

m \in ℝ

. Der Graph von

f

wird mit

G_{f}

und der Graph von

g_{m}

mit

G_{m}

bezeichnet.

Teilaufgabe Teil A 3a (3 BE)

Skizzieren Sie

G_{f}

in einem Koordinatensystem. Berechnen Sie die Koordinaten des gemeinsamen Punkts der Graphen

G_{f}

und

G_{4}

Teilaufgabe Teil A 3b (2 BE)

Es gibt Werte von

m

, für die die Graphen

G_{f}

und

G_{m}

jeweils keinen gemeinsamen Punkt haben. Geben Sie diese Werte von

m

an.

Gegeben ist die Funktion

g

mit

g (x) = 0, 7 \cdot e^{0, 5 x} - 0, 7

und

x \in ℝ

. Die Funktion

g

ist umkehrbar. Die Abbildung 2 zeigt den Graphen

G_{g}

von

g

sowie einen Teil des Graphen

G_{h}

der Umkehrfunktion

h

von

g

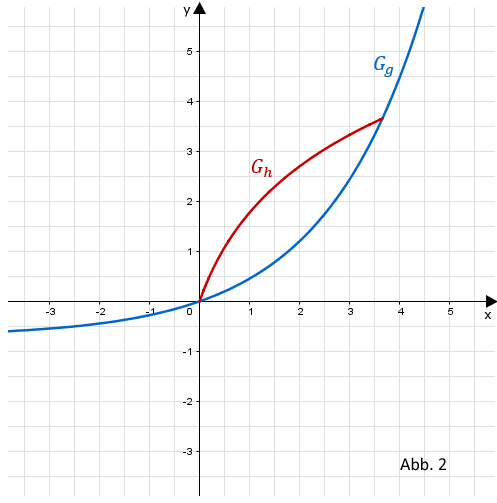
Teilaufgabe Teil A 4a (2 BE)

Zeichnen Sie in die Abbildung 2 den darin fehlenden Teil von

G_{h}

ein.

Teilaufgabe Teil A 4b (2 BE)

Betrachtet wird das von den Graphen

G_{g}

und

G_{h}

eingeschlossene Flächenstück. Schraffieren Sie den Teil dieses Flächenstücks, dessen Inhalt mit dem Term

2 \cdot \int_{0}^{2, 5} (x - g (x)) dx

berechnet werden kann.

Teilaufgabe Teil A 4c (2 BE)

Geben Sie den Term einer Stammfunktion der in

ℝ

definierten Funktion

k : x \mapsto x - g (x)

an.

Gegeben ist die in

ℝ

definierte Funktion

f : x \mapsto \frac{x^{2} - 1}{x^{2} + 1}

; die Abbildung 1 (Teil B) zeigt ihren Graphen

G_{f}

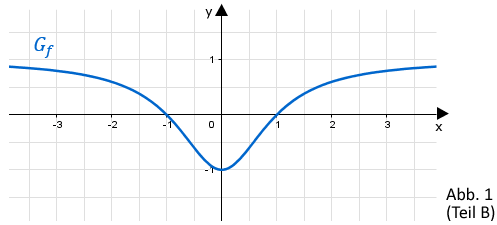
Teilaufgabe Teil B 1a (5 BE)

Bestätigen Sie rechnerisch, dass

G_{f}

symmetrisch bezüglich der

y

-Achse ist, und untersuchen Sie anhand des Funktionsterms das Verhalten von

f

für

x \to + \infty

. Bestimmen Sie diejenigen

x

-Werte, für die

f (x) = 0, 96

gilt.

Teilaufgabe Teil B 1b (4 BE)

Untersuchen Sie rechnerisch das Monotonieverhalten von

G_{f}

.

(zur Kontrolle:

f^{'} (x) = \frac{4 x}{{(x^{2} + 1)}^{2}}

)

Teilaufgabe Teil B 1c (4 BE)

Bestimmen Sie rechnerisch eine Gleichung der Tangente

t

G_{f}

im Punkt

(3 | f (3))

. Berechnen Sie die Größe des Winkels, unter dem

t

die x-Achse schneidet, und zeichnen Sie

t

in die Abbildung 1 (Teil B) ein.

Nun wird die in

ℝ

definierte Integralfunktion

F : x \mapsto \int_{0}^{x} f (t) dt

betrachtet; ihr Graph wird mit

G_{F}

bezeichnet.

Teilaufgabe Teil B 2a (5 BE)

Begründen Sie, dass

F

x = 0

eine Nullstelle hat, und machen Sie mithilfe des Verlaufs von

G_{f}

plausibel, dass im Intervall

[1; 3]

eine weitere Nullstelle von

F

liegt.
Geben Sie an, welche besondere Eigenschaft

G_{F}

im Punkt

(- 1 | F (- 1))

hat, und begründen Sie Ihre Angabe.

Teilaufgabe Teil B 2b (2 BE)

Die Gerade mit der Gleichung

y = x - 1

begrenzt gemeinsam mit den Koordinatenachsen ein Dreieck. Geben Sie den Flächeninhalt dieses Dreiecks und den sich daraus ergebenden Näherungswert für

F (1)

an.

Teilaufgabe Teil B 2c (5 BE)

Die Abbildung 2 (Teil B) zeigt den Graphen

G_{f}

sowie den Graphen

G_{g}

der in

ℝ

definierten Funktion

g : x \mapsto - \cos (\frac{π}{2} x)

.
Beschreiben Sie, wie

G_{g}

aus dem Graphen der in

ℝ

definierten Funktion

x \mapsto \cos x

hervorgeht, und berechnen Sie durch Integration von

g

einen weiteren Näherungswert für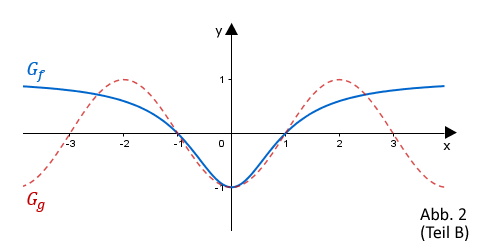

F (1)

(zur Kontrolle:

F (1) \approx - \frac{2}{π}

)

Teilaufgabe Teil B 2d (4 BE)

Berechnen Sie das arithmetische Mittel der beiden in den Aufgaben 2b und 2c berechneten Näherungswerte. Skizzieren Sie den Graphen von

F

für

0 \leq x \leq 3

unter Berücksichtigung der bisherigen Ergebnisse in der Abbildung 1 (Teil B).

Für jeden Wert

k > 0

legen die auf

G_{f}

liegenden Punkte

P_{k} (- k | f (- k))

und

Q_{k} (k | f (k))

gemeinsam mit dem Punkt

R (0 | 1)

ein gleichschenkliges Dreieck

P_{k} Q_{k} R

fest.

Teilaufgabe Teil B 3a (5 BE)

Berechnen Sie für

k = 2

den Flächeninhalt des zugehörigen Dreiecks

P_{2} Q_{2} R

(vgl. Abbildung 3).
Zeigen Sie anschließend, dass der Flächeninhalt des Dreiecks

P_{k} Q_{k} R

allgemein durch den Term

A (k) = \frac{2 k}{k^{2} + 1}

beschrieben werden kann.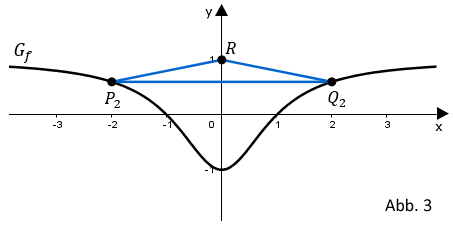

Teilaufgabe Teil B 3b (6 BE)

Zeigen Sie, dass es einen Wert von

k > 0

gibt, für den

A (k)

maximal ist. Berechnen Sie diesen Wert von

k

sowie den Flächeninhalt des zugehörigen Dreiecks

P_{k} Q_{k} R

Alle Abituraufgaben

Lösungen zu:

Teilaufgabe Teil A 1a

Teilaufgabe Teil A 1b

Teilaufgabe Teil A 2a

Teilaufgabe Teil A 2b

Teilaufgabe Teil A 3a

Teilaufgabe Teil A 3b

Teilaufgabe Teil A 4a

Teilaufgabe Teil A 4b

Teilaufgabe Teil A 4c

Teilaufgabe Teil B 1a

Teilaufgabe Teil B 1b

Teilaufgabe Teil B 1c

Teilaufgabe Teil B 2a

Teilaufgabe Teil B 2b

Teilaufgabe Teil B 2c

Teilaufgabe Teil B 2d

Teilaufgabe Teil B 3a

Teilaufgabe Teil B 3b

Lösung als Video:

Themen-Übersicht

Tipp:

Arbeite frühzeitig mit der Merkhilfe Mathematik,
die als Hilfsmittel im Abitur zugelassen ist.

Feedback:

Du hast einen Fehler gefunden oder hast Anregungen zur Internetseite?

Teile uns Dein Feedback mit!