Abitur 2020 Mathematik Analytische Geometrie VI

Gegeben sind die Punkte

P (- 2 | 3 | 0)

R (2 | - 1 | 2)

und

Q (q | 1 | 5)

mit der reellen Zahl

q

, wobei

Q

von

P

genauso weit entfernt ist wie von

R

Teilaufgabe Teil A 1a (3 BE)

Bestimmen Sie

q

.

(zur Kontrolle:

q = - 2

)

Teilaufgabe Teil A 1b (2 BE)

Ermitteln Sie die Koordinaten des Eckpunkts

S

der Raute

PQRS

. Zeigen Sie, dass

PQRS

kein Quadrat ist.

Gegeben sind in einem kartesischen Koordinatensystem die Ebene

E : 4 x_{1} - 8 x_{2} + x_{3} + 50 = 0

und die Gerade

g : \vec{X} = (\begin{matrix} 3 \\ 12 \\ - 2 \end{matrix}) + λ \cdot (\begin{matrix} 5 \\ 11 \\ - 4 \end{matrix})

λ \in ℝ

Teilaufgabe Teil B a (1 BE)

Erläutern Sie, warum die folgende Rechnung ein Nachweis dafür ist, dass

g

und

E

genau einen gemeinsamen Punkt haben:

(\begin{matrix} 4 \\ - 8 \\ 1 \end{matrix}) \circ (\begin{matrix} 5 \\ 11 \\ - 4 \end{matrix}) = - 72 \neq 0

Teilaufgabe Teil B b (5 BE)

Berechnen Sie die Größe des Schnittwinkels von

g

und

E

und zeigen Sie, dass

S (0, 5 | 6, 5 | 0)

der Schnittpunkt von

g

und

E

ist.

Teilaufgabe Teil B c (6 BE)

Die Kugel

K

mit dem Mittelpunkt

M (- 13 | 20 | 0)

berührt die Ebene

E

. Bestimmen Sie die Koordinaten des zugehörigen Berührpunkts

F

sowie den Kugelradius

r

.

(zur Kontrolle:

F (- 5 | 4 | 2)

r = 18

)

Teilaufgabe Teil B d (5 BE)

Weisen Sie nach, dass die Gerade

g

die Kugel

K

im Punkt

T (3 | 12 | - 2)

berührt.

Die Punkte

M

T

S

und

F

(vgl. die Aufgaben b, c und d) liegen in einer Ebene

Z

. Die nicht maßstabsgetreue Abbildung zeigt die Gerade

g

, den Schnitt der Ebene

E

mit der Ebene

Z

sowie den Schnitt der Kugel

K

mit der Ebene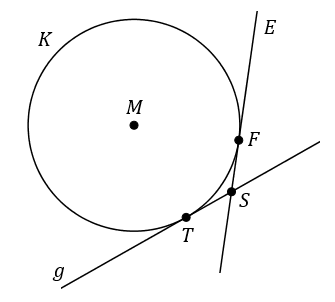

Z

Teilaufgabe Teil B e (4 BE)

Begründen Sie, dass das Viereck

MTSF

einen Umkreis besitzt.
Berechnen Sie den Flächeninhalt dieses Vierecks.

Teilaufgabe Teil B f (4 BE)

Durch Rotation des Vierecks

MTSF

um die Gerade

MS

entsteht ein Körper. Beschreiben Sie diesen Körper.
In einer Formelsammlung ist zur Berechnung des Volumens eines solchen Körpers die Formel

V = \frac{1}{3} \cdot {(\frac{a}{2})}^{2} \cdot π \cdot b

zu finden. Geben Sie für den beschriebenen Körper die Strecken an, deren Längen für

a

bzw.

b

einzusetzen sind.

Alle Abituraufgaben

Lösungen zu:

Teilaufgabe Teil A 1a

Teilaufgabe Teil A 1b

Teilaufgabe Teil B a

Teilaufgabe Teil B b

Teilaufgabe Teil B c

Teilaufgabe Teil B d

Teilaufgabe Teil B e

Teilaufgabe Teil B f

Lösung als Video:

Themen-Übersicht

Tipp:

Arbeite frühzeitig mit der Merkhilfe Mathematik,
die als Hilfsmittel im Abitur zugelassen ist.

Feedback:

Du hast einen Fehler gefunden oder hast Anregungen zur Internetseite?

Teile uns Dein Feedback mit!