über 250 kostenlose
Abituraufgaben
Lösung als Video
und ausformuliert
Alle Lösungen von
erfahrenen Lehrern
Abitur 2020 Mathematik Analytische Geometrie V
Die Strecke mit den Endpunkten und ist Durchmesser einer Kugel mit Mittelpunkt .
Teilaufgabe Teil A a (3 BE)
Berechnen Sie die Koordinaten von und weisen Sie nach, dass der Punkt auf der Kugel liegt.
Teilaufgabe Teil A b (2 BE)
Begründen Sie ohne weitere Rechnung, dass das Dreieck bei rechtwinklig ist.
| Die Abbildung 1 zeigt modellhaft eine Mehrzweckhalle, die auf einer horizontalen Fläche steht und die Form eines geraden Prismas hat. Die Punkte , , und stellen im Modell die Eckpunkte der Grundfläche der Mehrzweckhalle dar, die Punkte , , und die Eckpunkte der Dachfläche. Diejenige Seitenwand, die im Modell in der -Ebene liegt, ist 6 m hoch, die ihr gegenüberliegende Wand nur 4 m. | 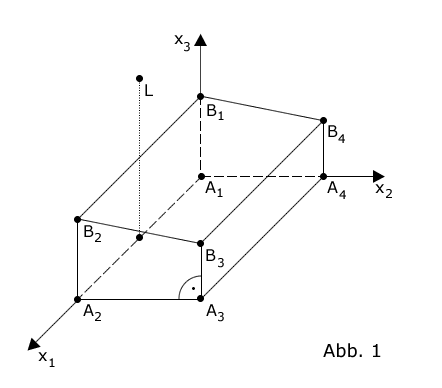 |
Teilaufgabe Teil B a (4 BE)
Geben Sie die Koordinaten der Punkte , und an und bestätigen Sie, dass diese Punkte in der Ebene liegen.
Teilaufgabe Teil B b (3 BE)
Berechnen Sie die Größe des Neigungswinkels der Dachfläche gegenüber der Horizontalen.
Teilaufgabe Teil B c (6 BE)
Der Punkt liegt auf der Kante . Untersuchen Sie rechnerisch, ob es Punkte auf der Kante gibt, für die gilt: Die Verbindungsstrecken des Punktes zu den Punkten und stehen aufeinander senkrecht. Geben Sie gegebenenfalls die Koordinaten dieser Punkte an.
Der Punkt , der vertikal über dem Mittelpunkt der Kante liegt, veranschaulicht im Modell die Position einer Flutlichtanlage, die 12 m über der Grundfläche angebracht ist. Die als punktförmig angenommene Lichtquelle beleuchtet – mit Ausnahme des Schattenbereichs in der Nähe der Hallenwände – das gesamte Gelände um die Halle.
Teilaufgabe Teil B d (5 BE)
Die Punkte , und legen eine Ebene fest. Ermitteln Sie eine Gleichung von in Normalenform.
(zur Kontrolle: )
(zur Kontrolle: )
Teilaufgabe Teil B e (3 BE)
Die Ebene schneidet die -Ebene in der Gerade . Bestimmen Sie eine Gleichung von .
(zur Kontrolle: , )
(zur Kontrolle: , )
Teilaufgabe Teil B f (4 BE)
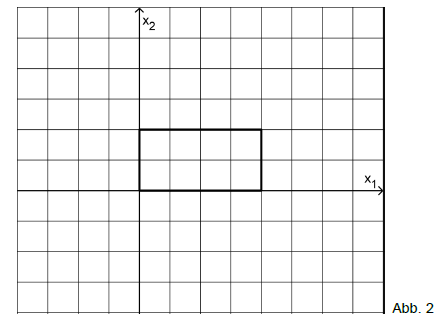
Die Abbildung 2 zeigt den Grundriss des Hallenmodells in der -Ebene. Stellen Sie unter Verwendung der bisherigen Ergebnisse den Schattenbereich der Flutlichtanlage in der Abbildung exakt dar.

Lösungen zu:
Tipp:
Arbeite frühzeitig mit der Merkhilfe Mathematik,
die als Hilfsmittel im Abitur zugelassen ist.
die als Hilfsmittel im Abitur zugelassen ist.
Feedback:
Du hast einen Fehler gefunden oder hast Anregungen zur Internetseite?








