über 250 kostenlose
Abituraufgaben
Lösung als Video
und ausformuliert
Alle Lösungen von
erfahrenen Lehrern
Abitur 2018 Mathematik Analytische Geometrie V
Gegeben ist die Kugel mit Mittelpunkt und Radius .
Teilaufgabe Teil A 1a (3 BE)
Bestimmen Sie alle Werte , für die der Punkt auf der Kugel liegt.
Teilaufgabe Teil A 1b (2 BE)
Die Gerade berührt die Kugel im Punkt . Ermitteln Sie eine mögliche Gleichung von .
Für jeden Wert von mit ist eine Gerade gegeben durch
,
,
Teilaufgabe Teil A 2a (2 BE)
Bestimmen Sie in Abhängigkeit von die Koordinaten des Punkts, in dem die -Ebene schneidet.
Teilaufgabe Teil A 2b (3 BE)
Für genau einen Wert von hat die Gerade einen Schnittpunkt mit der -Achse. Ermitteln Sie die Koordinaten dieses Schnittpunkts.
Auf einem Spielplatz wird ein dreieckiges Sonnensegel errichtet, um einen Sandkasten zu beschatten. Hierzu werden an drei Ecken des Sandkastens Metallstangen im Boden befestigt, an deren Enden das Sonnensegel fixiert wird.
In einem kartesischen Koordinatensystem stellt die -Ebene den horizontalen Boden dar. Der Sandkasten wird durch das Rechteck mit den Eckpunkten , , und beschrieben. Das Sonnensegel wird durch das ebene Dreieck mit den Eckpunkten , und dargestellt (vgl. Abbildung 1). Eine Längeneinheit im Koordinatensystem entspricht einem Meter in der Realität.
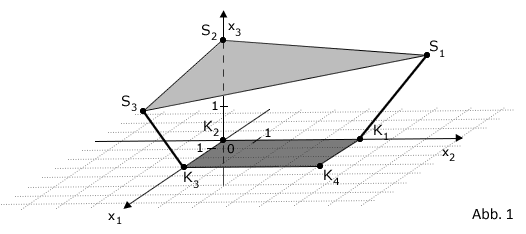
In einem kartesischen Koordinatensystem stellt die -Ebene den horizontalen Boden dar. Der Sandkasten wird durch das Rechteck mit den Eckpunkten , , und beschrieben. Das Sonnensegel wird durch das ebene Dreieck mit den Eckpunkten , und dargestellt (vgl. Abbildung 1). Eine Längeneinheit im Koordinatensystem entspricht einem Meter in der Realität.

Die drei Punkte , und legen die Ebene fest.
Teilaufgabe Teil B a (4 BE)
Ermitteln Sie eine Gleichung der Ebene in Normalenform.
(zur Kontrolle: )
(zur Kontrolle: )
Teilaufgabe Teil B b (3 BE)
Der Hersteller des Sonnensegels empfiehlt, die verwendeten Metallstangen bei einer Sonnensegelfläche von mehr als durch zusätzliche Sicherungsseile zu stabilisieren. Beurteilen Sie, ob eine solche Sicherung aufgrund dieser Empfehlung in der vorliegenden Situation nötig ist.
Auf das Sonnensegel fallen Sonnenstrahlen, die im Modell und in der Abbildung 1 durch parallele Geraden mit dem Richtungsvektor dargestellt werden können. Das Sonnensegel erzeugt auf dem Boden einen dreieckigen Schatten. Die Schatten der mit bzw. bezeichneten Ecken des Sonnensegels werden mit bzw. bezeichnet.
Teilaufgabe Teil B c (2 BE)
Begründen Sie ohne weitere Rechnung, dass auf der -Achse liegt.
Teilaufgabe Teil B d (3 BE)
hat die Koordinaten . Zeichnen Sie das Dreieck, das den Schatten des Sonnensegels darstellt, in Abbildung 1 ein. Entscheiden Sie anhand der Zeichnung, ob mehr als die Hälfte des Sandkastens beschattet ist.
Teilaufgabe Teil B e (3 BE)
Um das Abfließen von Regenwasser sicherzustellen, muss das Sonnensegel einen Neigungswinkel von mindestens gegenüber dem horizontalen Boden aufweisen. Begründen Sie, dass das Abfließen von Regenwasser im vorliegenden Fall nicht sichergestellt ist.
Teilaufgabe Teil B f (5 BE)
Bei starkem Regen verformt sich das Sonnensegel und hängt durch. Es bildet sich eine sogenannte Wassertasche aus Regenwasser, das nicht abfließen kann. Die Oberseite der Wassertasche verläuft horizontal und ist näherungsweise kreisförmig mit einem Durchmesser von . An ihrer tiefsten Stelle ist die Wassertasche tief. Vereinfachend wird die Wassertasche als Kugelsegment betrachtet (vgl. Abbildung 2).
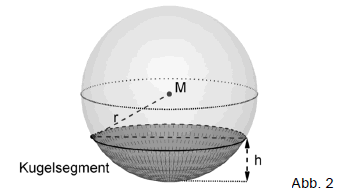
Das Volumen eines Kugelsegments kann mit der Formel berechnet werden, wobei den Radius der Kugel und die Höhe des Kugelsegments bezeichnen. Ermitteln Sie, wie viele Liter Wasser sich in der Wassertasche befinden.

Das Volumen eines Kugelsegments kann mit der Formel berechnet werden, wobei den Radius der Kugel und die Höhe des Kugelsegments bezeichnen. Ermitteln Sie, wie viele Liter Wasser sich in der Wassertasche befinden.
Lösungen zu:
Tipp:
Arbeite frühzeitig mit der Merkhilfe Mathematik,
die als Hilfsmittel im Abitur zugelassen ist.
die als Hilfsmittel im Abitur zugelassen ist.
Feedback:
Du hast einen Fehler gefunden oder hast Anregungen zur Internetseite?








