über 180 kostenlose
Abituraufgaben
Lösung als Video
und ausformuliert
Alle Lösungen von
erfahrenen Lehrern
 
 
 
 
Bitte einloggen oder einmalig kostenlos registrieren, um die Lösung dieser Aufgabe betrachten zu können.
 
Wir hoffen, dass wir Dir bei Deiner Vorbereitung auf das Mathe-Abitur helfen konnten und wünschen viel Erfolg beim Abitur!

Bitte hilf uns Abiturloesung.de zu verbessern und nimm an unserer Umfrage teil.
 
Abitur 2011 G9 Abitur Mathematik LK Infinitesimalrechnung II
Gegeben ist die Funktion f : x ↦ 2 x ⋅ ln ( x 2 ) mit Definitionsbereich R + . Der Graph von f wird mit G f bezeichnet.
Teilaufgabe 1a  (4 BE)

Bestimmen Sie die Nullstelle von f und geben Sie das Verhalten von f an den Rändern des Definitionsbereichs an.

Teilaufgabe 1b  (8 BE)

Bestimmen Sie Lage und Art des Extrempunkts E ( x E | y E ) sowie das Krümmungsverhalten von G f .

[Teilergebnis: x E = 2 e ]


Teilaufgabe 1c  (5 BE)

Geben Sie das Verhalten von f ′ ( x ) für x → 0 an. Berechnen Sie f ( 3 ) und zeichnen Sie G f unter Verwendung der bisherigen Ergebnisse in ein Koordinatensystem ein.

Die Einschränkung von f auf das Intervall ] 0 ; x E ] besitzt die Umkehrfunktion g 1 , die Einschränkung von f auf das Intervall [ x E ; + ∞ [ die Umkehrfunktion g 2 .
Teilaufgabe 1d  (5 BE)

Die Graphen von f und g 2 haben den Punkt S ( x S | y S ) gemeinsam. Berechnen Sie die Koordinaten von S . Zeichnen Sie die Graphen von g 1 und g 2 in das Koordinatensystem aus Teilaufgabe 1c ein.

[Teilergebnis: x S = 2 e ]


Teilaufgabe 1e  (4 BE)

Ermitteln Sie den Term einer Stammfunktion F von f .

[mögliches Ergebnis: F ( X ) = x 2 ⋅ ln ( x 2 ) - 1 2 x 2 ]


Teilaufgabe 1f  (5 BE)

Die Graphen von f , g 1 und g 2 bilden, ergänzt durch den Koordinatenursprung, den Rand eines endlichen Flächenstücks. Berechnen Sie den Inhalt dieses Flächenstücks.

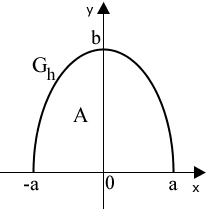
Der Graph G h der in [ - a ; a ] definierten Funktion h ist eine halbe Ellipse, die die y -Achse im Punkt ( 0 | b ) schneidet und mit der x -Achse ein Flächenstück des Inhalts A einschließt ( a , b ∈ R + ; siehe Abbildung). Der Funktionsterm von h wird im Folgenden nicht benötigt.

Teilaufgabe 2a  (4 BE)

Weisen Sie nach, dass für jede reelle Zahl r die Beziehung

π ∫ - a a ( h ( x ) + r ) 2 d x - π ∫ - a a ( - h ( x ) + r ) 2 d x = 2 π r ⋅ 2 A

gilt, indem Sie die linke Seite der Gleichung geeignet umformen.

Teilaufgabe 2b  (5 BE)

Geben Sie an, wie die Graphen der in [ - a ; a ] definierten Funktionen h 1 : x ↦ h ( x ) + r und h 2 : x ↦ - h ( x ) + r aus G h hervorgehen.
Durch den Term auf der linken Seite der Gleichung aus Teilaufgabe 2a wird für r > b das Volumen eines Rotationskörpers beschrieben. Für welchen der abgebildeten Gegenstände stellt dieser Rotationskörper bei passender Wahl von a und b ein geeignetes Modell dar? Begründen Sie Ihre Antwort.


Lösung als Video:

 
Unsere Apps:
NEU:Themen-Übersicht
Themen
Tipp:
Arbeite frühzeitig mit der Merkhilfe Mathematik,
die als Hilfsmittel im Abitur zugelassen ist.
Feedback:
Du hast einen Fehler gefunden oder hast Anregungen zur Internetseite?