über 180 kostenlose
Abituraufgaben
Lösung als Video
und ausformuliert
Alle Lösungen von
erfahrenen Lehrern
 
 
 
 
Abitur 2010 Mathematik LK Infinitesimalrechnung I
Gegeben ist die Schar der Funktionen f k : ↦ x - ln x k mit k ∈ R + und Definitionsmenge D = R + . Der Graph von f k wird mit G k bezeichnet.
Teilaufgabe 1a  (3 BE)

Untersuchen Sie das Verhalten von f k für x → 0 und für x → ∞ .

Teilaufgabe 1b  (8 BE)

Bestimmen Sie Lage und Art des Extrempunktes von G k sowie das Krümmungsverhalten von G k . Berechnen Sie f 1 ( 6 ) und skizzieren Sie G 1 in ein geeignetes Koordinatensystem.
[zur Kontrolle: Tiefpunkt bei x = 1 ]

Teilaufgabe 1c  (6 BE)

Zeigen Sie, dass G k aus G 1 durch eine Verschiebung in Richtung der y -Achse hervorgeht.
Bestimmen Sie die Anzahl der Nullstellen von f k in Abhängigkeit von k . (Hinweis: Versuchen Sie nicht, die Nullstellen zu berechnen.)

Teilaufgabe 1d  (4 BE)

Begründen Sie, dass f k im Intervall ] 0 ; 1 ] umkehrbar ist, und geben Sie Definitions- und Wertemenge der zugehörigen Umkehrfunktion f k - 1 an. Geben Sie die Stelle an, an der f k - 1 nicht differenzierbar ist.

Teilaufgabe 1e  (7 BE)

Betrachtet wird folgende Aussage:

∫ 0 1 f k ( x ) d x = 1 , 5 + ln k

α ) Weisen Sie nach, dass die Aussage wahr ist.
β ) Interpretieren Sie die Aussage für k = 1 geometrisch.
γ ) Geben Sie ein Integral über f 1 - 1 an, dessen Wert Sie mit Hilfe der Aussage ermitteln können, und bestimmen Sie diesen Wert.

Teilaufgabe 1f  (3 BE)

In dieser Teilaufgabe werden diejenigen Funktionen f k betrachtet, deren Graphen G k die x -Achse jeweils in genau zwei Punkten schneiden. Durch G k , die beiden Koordinatenachsen sowie die Gerade x = 1 werden dann jeweils im Bereich x ≤ 1 zwei Flächenstücke endlichen Inhalts festgelegt, von denen das eine oberhalb, das andere unterhalb der x -Achse liegt. Bestimmen Sie k so, dass diese beiden Flächenstücke inhaltsgleich sind.

Gegeben ist eine in R definierte, zweimal differenzierbare Funktion g mit der Eigenschaft

g ′ ( x ) = g ( x ) ⋅ [ 1 - g ( x ) ] für alle x ∈ R .
Teilaufgabe 2a  (3 BE)

Zeigen Sie, dass für alle x ∈ R gilt:
g ′ ′ ( x ) = g ( x ) ⋅ [ 1 - g ( x ) ] ⋅ [ 1 - 2 ⋅ g ( x ) ]

Teilaufgabe 2b  (6 BE)

Einer der vier im Folgenden abgebildeten Graphen stellt den Graphen von g dar. Geben Sie an, welcher dies ist, und begründen Sie Ihre Antwort, indem Sie erklären, warum die anderen nicht in Betracht kommen.




Lösung als Video:

 
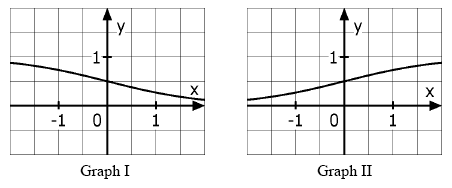
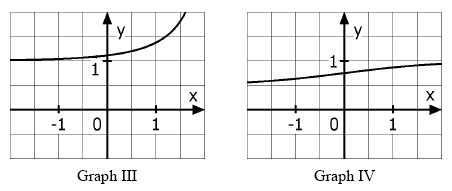
Jetzt auch als App:
Tipp:
Arbeite frühzeitig mit der Merkhilfe Mathematik,
die als Hilfsmittel im Abitur zugelassen ist.
Feedback:
Du hast einen Fehler gefunden oder hast Anregungen zur Internetseite?