über 250 kostenlose
Abituraufgaben
Lösung als Video
und ausformuliert
Alle Lösungen von
erfahrenen Lehrern

Abitur 2009 Mathematik LK Stochastik III

Eine kleine Pension mit 5 Gästezimmern im ersten Stock und 4 weiteren im zweiten Stock wird renoviert. Die individuell gestalteten Zimmer unterscheiden sich durch Lage, Größe und Ausstattung.
Für die Bäderrenovierung der Gästezimmer bestellt der Pensionsinhaber 2500 Fliesen. Aus Kostengründen entscheidet er sich für Fliesen II. Wahl, wobei der Verkäufer versichert, dass höchstens 10 % derartiger Fliesen fehlerhaft sind. Die Fliesen werden in Kartons zu je 50 Stück geliefert.
Teilaufgabe 1a  (3 BE)
Der Pensionsinhaber ist gegenüber der 10 % -Angabe skeptisch und vereinbart daher mit dem Verkäufer: Ein Karton aus der Lieferung wird zufällig ausgewählt und sein Inhalt geprüft. Wenn mehr als 5 Fliesen fehlerhaft sind, wird die Annahme der Lieferung verweigert, ansonsten akzeptiert. Mit welcher Wahrscheinlichkeit wird die Lieferung angenommen, obwohl im Mittel 15 % der Fliesen fehlerhaft sind?

Teilaufgabe 1b  (4 BE)
Die Wahrscheinlichkeit für eine fehlerhafte Fliese sei p . Wie würde die Entscheidungsregel mit einem möglichst großen Ablehnungsbereich lauten, wenn man die Nullhypothese H 0 : p > 0 , 1 anhand der 50 Fliesen eines Kartons auf dem Signifikanzniveau 5 % testen würde?

Im Folgendenist die Wahrscheinlichkeit für eine fehlerhafte Fliese 10 % . Verwenden Sie jeweils die Normalverteilung als Näherung.
Teilaufgabe 1c  (3 BE)
Berechnen Sie die Wahrscheinlichkeit dafür, dass von den 2500 Fliesen höchstens 260 fehlerhaft sind.

Teilaufgabe 1d  (7 BE)
Berechnen Sie die Grenzen eines möglichst kleinen Intervalls symmetrisch zum Erwartungswert, in dem die Anzahl fehlerhafter Fliesen der gesamten Lieferung mit einer Wahrscheinlichkeit von mindestens 95 % liegt.

Nach der Renovierung kommen die ersten 5 Übernachtungsgäste gleichzeitig an: 3 Frauen und 2 Männer. Jeder Gast möchte ein eigenes Zimmer.
Teilaufgabe 2a  (5 BE)
Die Gäste äußern unabhängig voneinander ihren Zimmerwunsch. Die Zimmerwahl ist nicht geglückt, wenn mindestens ein Zimmer mehrfach gewünscht wird. Wie viele Möglichkeiten gibt es, dass die Wahl nicht glückt, wenn nur danach unterschieden wird, wie oft ein Zimmer gewählt wurde?

Teilaufgabe 2b  (3 BE)
Die Gäste einigen sich schließlich darauf, dass die Zimmer der Frauen in einem der beiden Stockwerke liegen und die der Männer im anderen Stockwerk. Wie viele verschiedene Zimmerbelegungen sind möglich, wenn dabei auch nach den einzelnen Personen unterschieden wird?

Eine Zufallsgröße X mit der Wertemenge { 0 ; 1 ; 2 ; 3 } und Erwartungswert 1 hat folgende Verteilung:

P ( X = k ) = a - k a ⋅ b mit k ∈ { 0 ; 1 ; 2 ; 3 } und a , b ∈ ℝ + .
Teilaufgabe 3a  (5 BE)
Berechnen Sie a und b .

[Ergebnis: a = 4 ; b = 0 , 4 ]

Teilaufgabe 3b  (4 BE)
Begründen Sie, dass X nicht die Anzahl der Treffer einer binomial verteilten Zufallsgröße beschreiben kann.

Teilaufgabe 3c  (6 BE)
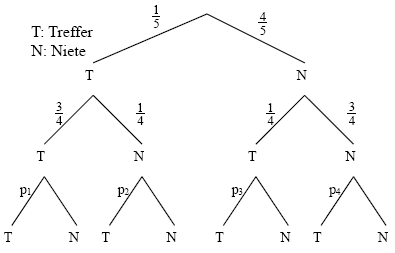
Die Zufallsgröße X gibt die Anzahl der Treffer bei einem dreistufigen Zufallsexperiment an. Dieses Zufallsexperiment wird durch das unten stehende Baumdiagramm beschrieben.
Berechnen Sie p 1 und p 4 und ermitteln Sie je einen möglichen Wert für p 2 und p 3 so, dass sich mit diesen vier Werten die Verteilung der Zufallsgröße X ergibt.


Alle Abituraufgaben
Lösungen zu:
Teilaufgabe 1a
Teilaufgabe 1b
Teilaufgabe 1c
Teilaufgabe 1d
Teilaufgabe 2a
Teilaufgabe 2b
Teilaufgabe 3a
Teilaufgabe 3b
Teilaufgabe 3c
Lösung als Video:
Themen-Übersicht
Themen
Tipp:
Arbeite frühzeitig mit der Merkhilfe Mathematik,
die als Hilfsmittel im Abitur zugelassen ist.
Feedback:

Du hast einen Fehler gefunden oder hast Anregungen zur Internetseite?

Teile uns Dein Feedback mit!