über 250 kostenlose
Abituraufgaben
Lösung als Video
und ausformuliert
Alle Lösungen von
erfahrenen Lehrern
Abitur 2016 Mathematik Analytische Geometrie V
| Betrachtet wird der abgebildete Würfel . Die Eckpunkte , , und dieses Würfels besitzen in einem kartesischen Koordinatensystem die folgenden Koordinaten: , , und . | 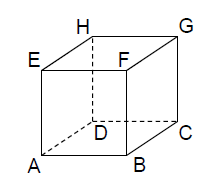 |
Teilaufgabe Teil A 1a (2 BE)
Zeichnen Sie in die Abbildung die Koordinatenachsen ein und bezeichnen Sie diese. Geben Sie die Koordinaten des Punkts an.
Teilaufgabe Teil A 1b (3 BE)
Der Punkt liegt auf der Kante des Würfels und hat vom Punkt den Abstand 3. Berechnen Sie die Koordinaten des Punkts .
Gegeben sind die Punkte und .
Teilaufgabe Teil A 2a (2 BE)
Bestimmen Sie die Koordinaten des Punkts so, dass gilt: .
Teilaufgabe Teil A 2b (3 BE)
Durch die Punkte und verläuft die Gerade .
Betrachtet werden Geraden, für welche die Bedingungen I und II gelten:
I Jede dieser Geraden schneidet die Gerade orthogonal.
II Der Abstand jeder dieser Geraden vom Punkt beträgt 3.
Ermitteln Sie eine Gleichung für eine dieser Geraden.
Betrachtet werden Geraden, für welche die Bedingungen I und II gelten:
I Jede dieser Geraden schneidet die Gerade orthogonal.
II Der Abstand jeder dieser Geraden vom Punkt beträgt 3.
Ermitteln Sie eine Gleichung für eine dieser Geraden.
In einem kartesischen Koordinatensystem legen die Punkte , und das gleichseitige Dreieck fest.
Teilaufgabe Teil B a (4 BE)
Ermitteln Sie eine Gleichung der Ebene , in der das Dreieck liegt, in Normalenform.
[mögliches Ergebnis: ]
[mögliches Ergebnis: ]
Spiegelt man die Punkte , und am Symmetriezentrum , so erhält man die Punkte , bzw. .
Teilaufgabe Teil B b (3 BE)
Beschreiben Sie die Lage der Ebene, in der die Punkte , und liegen, im Koordinatensystem. Zeigen Sie, dass die Strecke senkrecht auf dieser Ebene steht.
Teilaufgabe Teil B c (4 BE)
Begründen Sie, dass das Viereck ein Quadrat mit der Seitenlänge ist.
| Der Körper ist ein sogenanntes Oktaeder. Er besteht aus zwei Pyramiden mit dem Quadrat als gemeinsamer Grundfläche und den Pyramidenspitzen bzw. . | 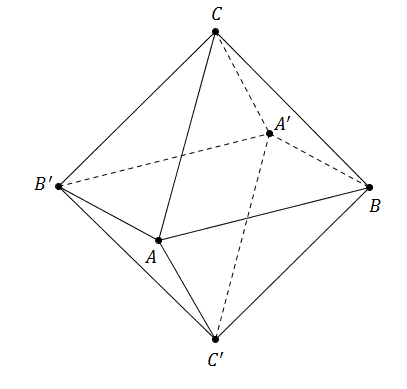 |
Teilaufgabe Teil B d (2 BE)
Weisen Sie nach, dass das Oktaeder das Volumen 36 besitzt.
Teilaufgabe Teil B e (4 BE)
Bestimmen Sie die Größe des Winkels zwischen den Seitenflächen und .
Teilaufgabe Teil B f (3 BE)
Alle Eckpunkte des Oktaeders liegen auf einer Kugel. Geben Sie eine Gleichung dieser Kugel an.
Berechnen Sie den Anteil des Oktaedervolumens am Kugelvolumen.
Berechnen Sie den Anteil des Oktaedervolumens am Kugelvolumen.
Lösungen zu:
Tipp:
Arbeite frühzeitig mit der Merkhilfe Mathematik,
die als Hilfsmittel im Abitur zugelassen ist.
die als Hilfsmittel im Abitur zugelassen ist.
Feedback:
Du hast einen Fehler gefunden oder hast Anregungen zur Internetseite?








