Abitur 2015 Mathematik NT Infinitesimalrechnung A II

Gegeben sind die ganzrationalen Funktionen

f_{a} : x \mapsto a \cdot (x^{3} + 2 x^{2} - 7 x + 4)

mit

D_{f_{a}} = ℝ

a \in ℝ

und

a > 0

Teilaufgabe 1.1 (6 BE)

Zerlegen Sie

f_{a} (x)

in Linearfaktoren und geben Sie die Nullstellen der Funktion

f_{a}

mit der jeweiligen Vielfachheit an.

Teilaufgabe 1.2 (5 BE)

Berechnen Sie den Wert von

a

so, dass die Tangente an den Graphen der Funktion

f_{a}

an der Stelle

x = - 3

die y-Achse bei

y = 5

schneidet.

Nun wird

a = \frac{1}{8}

gesetzt. Die Funktion

f_{\frac{1}{8}}

wird im Folgenden mit

f

bezeichnet.
Es gilt:

f (x) = \frac{1}{8} (x^{3} + 2 x^{2} - 7 x + 4)

Teilaufgabe 2.1 (7 BE)

Ermitteln Sie die maximalen Monotonieintervalle sowie Art und Koordinaten der Extrempunkte des Graphen von

f

Teilaufgabe 2.2 (4 BE)

Berechnen Sie die Koordinaten des Punktes

P

, in dem der Graph der Funktion

f

am stärksten fällt.

Teilaufgabe 2.3 (4 BE)

Zeichnen Sie unter Mitverwendung vorliegender Ergebnisse den Graphen von

f

im Bereich

- 5 \leq x \leq 4

in ein kartesisches Koordinatensystem.

Gegeben ist ferner die quadratische Funktion

p

mit

p^{''} (x) = 1

für alle

x \in ℝ

Teilaufgabe 3.1 (5 BE)

Bestimmen Sie den Funktionsterm

p (x)

, wenn der Punkt

A (- 4 | 8)

auf der Parabel

G_{p}

und ihr Scheitel bei

x_{S} = - \frac{1}{8}

liegt.
[Mögliches Ergebnis:

p (x) = \frac{1}{2} (x^{2} + \frac{1}{4} x + 1)

]

Teilaufgabe 3.2 (9 BE)

Berechnen Sie die Koordinaten der gemeinsamen Punkte der Graphen der Funktionen

p

und

f

(mit

f

aus 2.1) und zeichnen Sie die Parabel

G_{p}

für

- 4 \leq x \leq 4

in das vorhandene Koordinatensystem ein.

Teilaufgabe 3.3 (2 BE)

Geben Sie die Lösung der Ungleichung

p (x) - f (x) > 0

an und erläutern Sie, was das Ergebnis für die Graphen

G_{f}

und

G_{p}

bedeutet.

Teilaufgabe 3.4 (5 BE)

Die Graphen

G_{f}

und

G_{p}

schließen im II. Quadranten des Koordinatensystems ein endliches Flächenstück ein. Markieren Sie dieses Flächenstück und berechnen Sie die Maßzahl seines Inhalts.

Das Dreieck

A B C

in untenstehender Abbildung rotiert um die y-Achse, und dabei entsteht ein Kegel. Der Punkt

A

ist der Ursprung des Koordinatensystems und der Punkt

B

liegt im I. Quadranten auf der Parabel

G_{q}

mit

q (x) = - x^{2} + 8 x

und

x \in ℝ

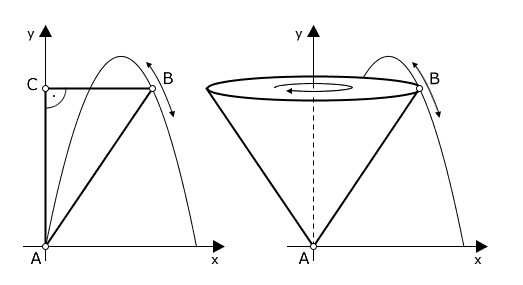
Teilaufgabe 4.1 (3 BE)

Stellen Sie eine Gleichung

V (r)

für das Volumen des Kegels auf, wobei

r = \bar{B C}

der Radius des Kegels ist.
[Mögliches Ergebnis:

V (r) = - \frac{1}{3} π r^{4} + \frac{8}{3} π r^{3}

]

Teilaufgabe 4.2 (3 BE)

Ermitteln Sie die maximale sinnvolle Definitionsmenge

D_{V}

der Funktion

V : r \mapsto V (r)

Teilaufgabe 4.3 (7 BE)

Bestimmen Sie die Koordinaten des Punktes

B

so, dass das Kegelvolumen seinen absolut größten Wert annimmt, und berechnen Sie das maximale Kegelvolumen.

Alle Abituraufgaben

Lösungen zu:

Teilaufgabe 1.1

Teilaufgabe 1.2

Teilaufgabe 2.1

Teilaufgabe 2.2

Teilaufgabe 2.3

Teilaufgabe 3.1

Teilaufgabe 3.2

Teilaufgabe 3.3

Teilaufgabe 3.4

Teilaufgabe 4.1

Teilaufgabe 4.2

Teilaufgabe 4.3

Lösung als Video:

Feedback:

Du hast einen Fehler gefunden oder hast Anregungen zur Internetseite?

Teile uns Dein Feedback mit!