über 250 kostenlose
Abituraufgaben
Lösung als Video
und ausformuliert
Alle Lösungen von
erfahrenen Lehrern
Abitur 2012 Mathematik NT Stochastik S I
Bei den folgenden Aufgaben sollen relative Häufigkeiten als Wahrscheinlichkeiten interpretiert werden.
Statistiken geben den Anteil der Linkshänder in der Bevölkerung mit Prozent an. In einer Fußgängerzone werden Passanten nach deren bevorzugter Schreibhand befragt.
Statistiken geben den Anteil der Linkshänder in der Bevölkerung mit Prozent an. In einer Fußgängerzone werden Passanten nach deren bevorzugter Schreibhand befragt.
Teilaufgabe 1.1 (4 BE)
Bestimmen Sie zum Beispiel mithilfe eines Baumdiagramms die
Wahrscheinlichkeit, dass man spätestens bei der dritten Befragung auf einen Linkshänder stößt.
Wahrscheinlichkeit, dass man spätestens bei der dritten Befragung auf einen Linkshänder stößt.
Teilaufgabe 1.2 (6 BE)
Bestimmen Sie die Wahrscheinlichkeit dafür, dass sich unter Befragten
a) genau Linkshänder
b) mindestens aber nicht mehr als Linkshänder
c) höchstens Linkshänder
d) genau zwei Linkshänder und diese in der Befragung nacheinander befinden.
a) genau Linkshänder
b) mindestens aber nicht mehr als Linkshänder
c) höchstens Linkshänder
d) genau zwei Linkshänder und diese in der Befragung nacheinander befinden.
In einer weiteren Befragung von zufällig ausgewählten Personen wurden genau Linkshänder () gezählt. Davon waren Frauen (). Die restlichen Frauen in der Befragung waren Rechtshänder. Die Auswahl einer Person und die Ermittlung ihrer Schreibhand und ihres Geschlechts wird als Zufallsexperiment aufgefasst.
Teilaufgabe 2.1 (4 BE)
Ermitteln Sie mithilfe einer Vierfeldertafel die Wahrscheinlichkeiten aller Elementarereignisse des Zufallsexperiments.
Teilaufgabe 2.2 (3 BE)
Beschreiben Sie das Ereignis möglichst einfach mit Worten und geben Sie dessen Wahrscheinlichkeit an.
Teilaufgabe 2.3 (3 BE)
Untersuchen Sie, ob die Ereignisse und stochastisch unabhängig sind und interpretieren Sie das Ergebnis im Sinne der vorliegenden Thematik.
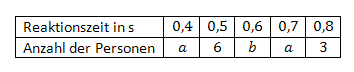
Linkshänder unterziehen sich einem Reaktionstest, bei welchem sie mit der rechten Hand beim Auftreten eines Ereignisses eine Taste betätigen. Folgende Tabelle zeigt, mit den Parametern , die gemessenen und auf Zehntelsekunden gerundeten Reaktionszeiten der Versuchspersonen:

Teilaufgabe 3.1 (4 BE)
Berechnen Sie die Werte und , wenn bekannt ist, dass genau Versuchspersonen höchstens Reaktionszeit benötigten.
[Teilergebnis: ]
[Teilergebnis: ]
Teilaufgabe 3.2 (3 BE)
Die Zufallsgröße gibt die Reaktionszeit einer zufällig herausgegriffenen Versuchsperson an.
Erstellen Sie die Wahrscheinlichkeitsverteilung der Zufallsgröße und stellen Sie sie geeignet graphisch dar.
Erstellen Sie die Wahrscheinlichkeitsverteilung der Zufallsgröße und stellen Sie sie geeignet graphisch dar.
Teilaufgabe 3.3 (5 BE)
Berechnen Sie, mit welcher Wahrscheinlichkeit die Zufallswerte innerhalb der einfachen Standardabweichung um den Erwartungswert liegen.
Eine Versuchsperson vermutet, dass mindestens der Linkshänder eine Reaktionszeit von maximal haben, wenn beim Reaktionstest die Taste mit der linken Hand betätigt wird (= Testkriterium). Eine zweite Versuchsperson ist weniger optimistisch (Gegenhypothese). Dazu wird ein Test mit Linkshändern durchgeführt.
Teilaufgabe 4.1 (6 BE)
Geben Sie für obigen Test die Testgröße sowie die Gegenhypothese an und bestimmen Sie den größtmöglichen Ablehnungsbereich der Nullhypothese auf dem -Niveau. Welche Entscheidung legt der Test nahe, wenn der Versuchspersonen das Testkriterium erfüllen?
Teilaufgabe 4.2 (2 BE)
Erläutern Sie, worin im vorliegenden Fall der Fehler 2. Art besteht.
Lösungen zu:
Lösung als Video:
delete-this-card
Feedback:
Du hast einen Fehler gefunden oder hast Anregungen zur Internetseite?






