Abitur 2011 Mathematik NT Infinitesimalrechnung A II

Gegeben ist die reelle Funktion

f : x \mapsto - \frac{1}{9} x^{4} + \frac{4}{3} x^{2} - 3

mit

D_{f} = ℝ

Teilaufgabe 1.1 (5 BE)

Berechnen Sie die Nullstellen der Funktion

f

und geben Sie das Symmetrieverhalten von

G_{f}

an.

Teilaufgabe 1.2 (6 BE)

Ermitteln Sie Art und Koordinaten der relativen Extrempunkte des Graphen der Funktion

f

Teilaufgabe 1.3 (6 BE)

Bestimmen Sie die maximalen Intervalle, in denen der Graph der Funktion

f

rechts- bzw. linksgekrümmt ist und berechnen Sie die Koordinaten der Wendepunkte.

Teilaufgabe 1.4 (5 BE)

Zeichnen Sie den Graphen der Funktion

f

im Bereich

- 3, 5 \leq x \leq 3, 5

mithilfe vorliegender Ergebnisse in ein Koordinatensystem.

Gegeben sind nun die reellen Funktionen

f_{a} : x \mapsto - \frac{1}{9} x^{4} + \frac{4}{3} x^{2} - a

mit

D_{f_{a}} = ℝ

und

a \in ℝ^{+}

.

Für

a = 3

erhält man die Funktion aus Aufgabe 1. Die Ergebnisse aus Aufgabe 1 können bei den folgenden Aufgaben verwendet werden.

Teilaufgabe 2.1 (3 BE)

Ermitteln Sie die Koordinaten aller relativer Extrempunkte des Graphen der Funktion

f_{a}

in Abhängigkeit von

a

Teilaufgabe 2.2 (6 BE)

Bestimmen Sie nur mithilfe der Ergebnisse aus 2.1 die Anzahl und Vielfachheiten der Nullstellen von

f_{a}

in Abhängigkeit von

a

Gegeben ist weiterhin die Funktion

p

durch

p (x) = - \frac{1}{3} x^{2} + 1

mit

D_{p} = ℝ

Teilaufgabe 3.1 (4 BE)

Zeigen Sie, dass

p

genau zwei gemeinsame Nullstellen mit der Funktion

f

aus Aufgabe 1 hat.
Zeichnen Sie den Graphen von

p

im Bereich

- 4 \leq x \leq 4

in das Koordinatensystem aus Teilaufgabe 1.4.

Teilaufgabe 3.2 (5 BE)

Die Graphen der Funktionen

f

(aus Aufgabe 1) und

p

schließen drei Flächenstücke ein. Berechnen Sie die Maßzahl desjenigen Flächenstücks, das den Ursprung enthält, auf zwei Nachkommastellen genau.

Teilaufgabe 3.3 (3 BE)

Die in 3.2 beschriebene Fläche stellt die Form eines Firmenlogos dar. Es soll aus einer dünnen Styroporplatte ausgesägt werden. Die Platte wird durch die Geraden mit den Gleichungen

x = - \sqrt{3}

x = \sqrt{3}

y = - 3

und

y = 1

von außen begrenzt. Berechnen Sie den Anteil des Abfalls nach dem Aussägen in Prozent.

Teilaufgabe 4 (7 BE)

Gegeben ist die reelle Funktion

H

durch

H (x) = - \frac{1}{108} x^{4} + a x^{3} + b x^{2} + c x + d

mit

a, b, c, d \in ℝ

H

ist eine Stammfunktion der ganzrationalen Funktion h.
Bestimmen Sie den Funktionsterm

H (x)

, wenn der Graph der Funktion

h

punktsymmetrisch zum Ursprung verläuft und

W (- 3 ∣ \frac{3}{4})

ein Wendepunkt des Graphen

G_{H}

ist.

Der Gepäckraum eines Flugzeugs kann im Querschnitt mithilfe der Funktion

p : x \mapsto 0, 5 x^{2} - 3, 125

beschrieben werden. Das Gepäck soll dabei in Containern mit rechteckiger Querschnittsfläche untergebracht werden (vgl. Abbildung).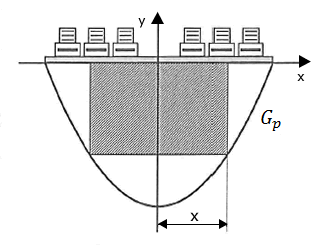

Die Längeneinheit ist Meter und kann bei den Berechnungen weggelassen werden.

Teilaufgabe 5.1 (4 BE)

Stellen Sie eine Gleichung für die Querschnittsfläche

A (x)

der Container in Abhängigkeit von

x

auf und bestimmen Sie eine im Sachzusammenhang sinnvolle Definitionsmenge.
[Teilergebnis:

A (x) = - x^{3} + 6, 25 x

]

Teilaufgabe 5.2 (6 BE)

Berechnen Sie

x

so, dass die Querschnittsfläche der Container den größten Inhalt annimmt. Berechnen Sie für diesen Fall auch die Breite und Höhe der Container.

Alle Abituraufgaben

Lösungen zu:

Teilaufgabe 1.1

Teilaufgabe 1.2

Teilaufgabe 1.3

Teilaufgabe 1.4

Teilaufgabe 2.1

Teilaufgabe 2.2

Teilaufgabe 3.1

Teilaufgabe 3.2

Teilaufgabe 3.3

Teilaufgabe 4

Teilaufgabe 5.1

Teilaufgabe 5.2

Lösung als Video:

Feedback:

Du hast einen Fehler gefunden oder hast Anregungen zur Internetseite?

Teile uns Dein Feedback mit!