über 250 kostenlose
Abituraufgaben
Lösung als Video
und ausformuliert
Alle Lösungen von
erfahrenen Lehrern
Abitur 2022 Mathematik Stochastik IV
Die Abbildung zeigt das Netz eines Würfels, von dem nur drei Seiten beschriftet sind.
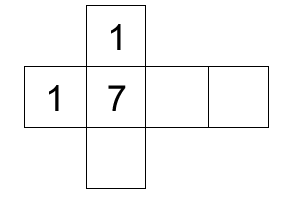

Teilaufgabe Teil A a (2 BE)
Der Würfel wird so lange geworfen, bis die Zahl 1 zum ersten Mal erzielt wird. Berechnen Sie die Wahrscheinlichkeit dafür, dass genau viermal gewürfelt wird.
Teilaufgabe Teil A b (3 BE)
Die drei leeren Seiten des Würfels sollen jeweils mit einer positiven geraden Zahl beschriftet werden. Ermitteln Sie eine Möglichkeit für die Beschriftung dieser drei Seiten, sodass bei einmaligem Werfen des Würfels der Erwartungswert für die erzielte Zahl beträgt.
Die SMV eines Gymnasiums initiierte im vergangenen Schuljahr die Aktionen "Baumpatenschaft" und "Umweltwoche".
Mit einer Umfrage auf dem Schulfest wird der Bekanntheitsgrad der beiden Aktionen ermittelt. Von den Befragten kennt jeder Fünfte die Aktion "Baumpatenschaft". der Befragten kennen keine der beiden Aktionen; die Aktion "Umweltwoche" kennen der Befragten nicht.
Aus den Befragten wird eine Person zufällig ausgewählt. Betrachtet werden folgende Ereignisse:
: "Die Person kennt die Aktion 'Baumpatenschaft'."
: "Die Person kennt die Aktion 'Umweltwoche'."
Aus den Befragten wird eine Person zufällig ausgewählt. Betrachtet werden folgende Ereignisse:
: "Die Person kennt die Aktion 'Baumpatenschaft'."
: "Die Person kennt die Aktion 'Umweltwoche'."
Teilaufgabe Teil B 1a (4 BE)
Weisen Sie nach, dass die Ereignisse und stochastisch unabhängig sind.
Teilaufgabe Teil B 1b (1 BE)
Geben Sie für den Fall, dass die ausgewählte Person die Aktion "Baumpatenschaft" kennt, die Wahrscheinlichkeit dafür an, dass sie die Aktion "Umweltwoche" nicht kennt.
Um Geld für die beiden Aktionen einzunehmen, bietet die SMV auf dem Schulfest das Spiel "2022" an. Bei dem Spiel werden zwei Glücksräder mit drei bzw. vier gleich großen Sektoren verwendet, die wie in Abbildung 1 beschriftet sind. Für einen Einsatz von 3 € darf man jedes der beiden Glücksräder einmal drehen. Für jede Ziffer 2, die auf den erzielten Sektoren steht, werden 2 € ausbezahlt. Die Zufallsgröße beschreibt, wie oft die Ziffer 2 auf den erzielten Sektoren insgesamt vorkommt.
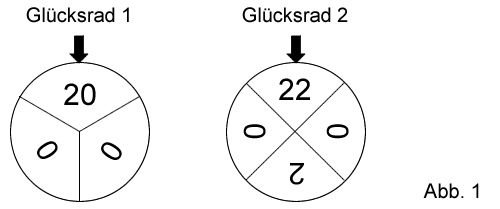

Teilaufgabe Teil B 2a (3 BE)
Die Tabelle zeigt die Wahrscheinlichkeitsverteilung von . Bestimmen Sie die Wahrscheinlichkeiten und .
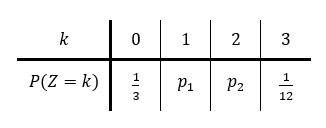
(zur Kontrolle: )
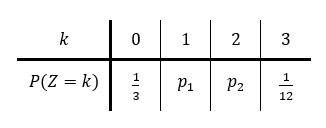
(zur Kontrolle: )
Teilaufgabe Teil B 2b (4 BE)
Ermitteln Sie, wie viele Spiele durchgeführt werden müssen, damit der Erwartungswert der Einnahme für die beiden Aktionen 300 € beträgt.
Acht Personen spielen nacheinander jeweils einmal das Spiel "2022".
Teilaufgabe Teil B 2c (4 BE)
Berechnen Sie die Wahrscheinlichkeit dafür, dass die SMV mehr als zweimal mindestens 4 € ausbezahlen muss.
Teilaufgabe Teil B 2d (3 BE)
Ermitteln Sie die Wahrscheinlichkeit dafür, dass an die ersten drei Personen drei unterschiedliche Beträge ausbezahlt werden, die in der Summe 12 € ergeben.
Die binomialverteilte Zufallsgröße mit den Parametern und besitzt die Standardabweichung . In Abbildung 2 ist die Wahrscheinlichkeitsverteilung von dargestellt.
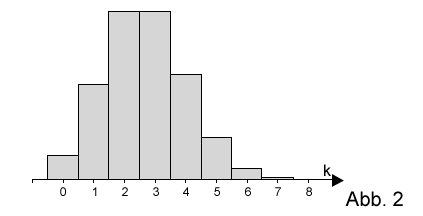

Teilaufgabe Teil B 3a (4 BE)
Ermitteln Sie den Wert des Parameters .
Teilaufgabe Teil B 3b (2 BE)
Die binomialverteilte Zufallsgröße hat die Parameter und
. Kennzeichnen Sie in Abbildung 2 eine Fläche, die die Wahrscheinlichkeit darstellt.
. Kennzeichnen Sie in Abbildung 2 eine Fläche, die die Wahrscheinlichkeit darstellt.
Lösungen zu:
Tipp:
Arbeite frühzeitig mit der Merkhilfe Mathematik,
die als Hilfsmittel im Abitur zugelassen ist.
die als Hilfsmittel im Abitur zugelassen ist.
Feedback:
Du hast einen Fehler gefunden oder hast Anregungen zur Internetseite?








