Abitur 2022 Mathematik Stochastik III

Gegeben sind die im Folgenden beschriebenen Zufallsgrößen

X

und

Y

Ein Würfel, dessen Seiten mit den Zahlen von 1 bis 6 durchnummeriert sind, wird zweimal geworfen. $X$ gibt die dabei erzielte Augensumme an.
Aus einem Behälter mit 60 schwarzen und 40 weißen Kugeln wird zwölfmal nacheinander jeweils eine Kugel zufällig entnommen und wieder zurückgelegt. $Y$ gibt die Anzahl der entnommenen schwarzen Kugeln an.

Teilaufgabe Teil A a (2 BE)

Begründen Sie, dass die Wahrscheinlichkeit

P (X = 4)

mit der Wahrscheinlichkeit

P (X = 10)

übereinstimmt.

Teilaufgabe Teil A b (3 BE)

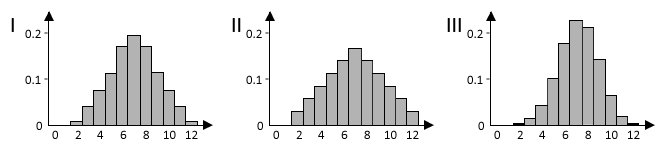
Die Wahrscheinlichkeitsverteilungen von

X

und

Y

werden jeweils durch eines der folgenden Diagramme I, II und III dargestellt. Ordnen Sie

X

und

Y

jeweils dem passenden Diagramm zu und begründen Sie Ihre Zuordnung.

Um die Wirksamkeit eines Pflanzenschutzmittels gegen Pilzbefall nachzuweisen, wurden zahlreiche Versuche durchgeführt, bei denen landwirtschaftliche Nutzpflanzen zunächst mit dem Pflanzenschutzmittel behandelt und anschließend mit Pilzsporen besprüht wurden. Im Mittel sind dabei

5 %

der Pflanzen von Pilzen befallen worden.

Bei einem weiteren solchen Versuch mit n Pflanzen beschreibt die Zufallsgröße

X_{n}

die Anzahl der Pflanzen, die von Pilzen befallen werden. Im Folgenden soll davon ausgegangen werden, dass

X_{n}

binomialverteilt ist mit den Parametern

n

und

p = 0, 05

Teilaufgabe Teil B 1a (6 BE)

Es werden 15 Pflanzen mit dem Pflanzenschutzmittel behandelt und anschließend mit Pilzsporen besprüht. Bestimmen Sie jeweils die Wahrscheinlichkeit folgender Ereignisse:

E_{1}

: "Keine der Pflanzen wird von Pilzen befallen."

E_{2}

: "Höchstens zwei Pflanzen werden von Pilzen befallen."

E_{3}

: "12 oder 13 Pflanzen bleiben ohne Pilzbefall."

Teilaufgabe Teil B 1b (4 BE)

Bestimmen Sie den kleinsten Wert von

n

, für den die Wahrscheinlichkeit dafür, dass mindestens eine Pflanze von Pilzen befallen wird, mindestens

99 %

beträgt.

Teilaufgabe Teil B 1c (4 BE)

Ermitteln Sie unter der Voraussetzung, dass bei einem Versuch mit 400 Pflanzen der Wert der Zufallsgröße

X_{400}

um höchstens eine Standardabweichung vom Erwartungswert abweicht, die kleinst- und die größtmögliche relative Häufigkeit der Pflanzen, die von Pilzen befallen werden.

Teilaufgabe Teil B 1d (3 BE)

Allgemein gilt für eine Zufallsgröße

X

mit Erwartungswert

μ

und Standardabweichung

σ

folgende Ungleichung für

k > 0

P (μ - k \cdot σ < X < μ + k \cdot σ) \geq 1 - \frac{1}{k^{2}}

Erläutern Sie die Aussage dieser Ungleichung für

k = 2

Um die Wirksamkeit des Pflanzenschutzmittels gegen einen nur in den Tropen auftretenden Pilz zu untersuchen, wurde ein Experiment mit 150 Pflanzen durchgeführt. Dabei wurden 70% der Pflanzen mit dem Pflanzenschutzmittel behandelt und anschließend alle 150 Pflanzen mit den Sporen des tropischen Pilzes besprüht.

Am Ende des Experiments war die Anzahl der unbehandelten Pflanzen ohne Pilzbefall dreimal so groß wie die Anzahl

x

der behandelten Pflanzen mit Pilzbefall. Insgesamt wurden 19 Pflanzen vom tropischen Pilz befallen.

Aus den 150 Pflanzen wird eine Pflanze zufällig ausgewählt. Betrachtet werden folgende Ereignisse:

S

: "Die Pflanze wurde mit dem Pflanzenschutzmittel behandelt."

T

: "Die Pflanze wurde vom tropischen Pilz befallen."

Teilaufgabe Teil B 2a (4 BE)

Bestimmen Sie x unter Zuhilfenahme einer Vierfeldertafel.

(zur Kontrolle:

x = 13

)

Teilaufgabe Teil B 2b (4 BE)

Berechnen Sie

P_{S} (T)

und

P_{\bar{S}} (T)

und begründen Sie, dass aus den Ergebnissen des Experiments nicht auf die Wirksamkeit des Pflanzenschutzmittels gegen den tropischen Pilz geschlossen werden kann.