über 250 kostenlose
Abituraufgaben
Lösung als Video
und ausformuliert
Alle Lösungen von
erfahrenen Lehrern
Abitur 2022 Mathematik Infinitesimalrechnung II
Gegeben ist die Funktion mit maximaler Definitionsmenge .
Teilaufgabe Teil A 1a (2 BE)
Geben Sie sowie eine Gleichung der waagrechten Asymptote des Graphen von an.
Teilaufgabe Teil A 1b (3 BE)
Zeigen Sie, dass der Graph von in genau einem Punkt eine waagrechte Tangente besitzt.
Betrachtet werden die in definierten Funktionen und , wobei eine Stammfunktion von ist. Abbildung 1 zeigt den Graphen von .
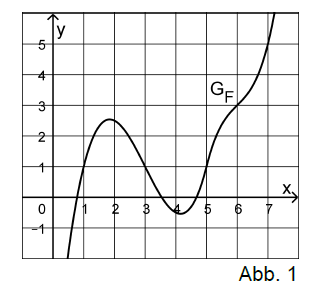

Teilaufgabe Teil A 2a (2 BE)
Bestimmen Sie den Wert des Integrals .
Teilaufgabe Teil A 2b (3 BE)
Bestimmen Sie den Funktionswert von an der Stelle 1; veranschaulichen Sie Ihr Vorgehen in Abbildung 1.
Teilaufgabe Teil A 3a (2 BE)
Gegeben ist die Funktion mit Definitionsmenge . Geben Sie die Nullstelle von sowie einen Term der ersten Ableitungsfunktion von an.
Teilaufgabe Teil A 3b (3 BE)
Die in definierte Funktion besitzt die Nullstelle , außerdem gilt für alle . Abbildung 2 zeigt den Graphen von .
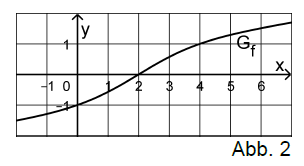
Betrachtet wird die Funktion mit maximaler Definitionsmenge . Geben Sie an und ermitteln Sie mithilfe von Abbildung 2 diejenige Stelle , für die gilt.

Betrachtet wird die Funktion mit maximaler Definitionsmenge . Geben Sie an und ermitteln Sie mithilfe von Abbildung 2 diejenige Stelle , für die gilt.
Gegeben sind die in definierten Funktionen mit und .
Teilaufgabe Teil A 4a (1 BE)
Zeigen Sie, dass gilt.
Teilaufgabe Teil A 4b (4 BE)
Betrachtet wird die Tangente an den Graphen von im Punkt .
Bestimmen Sie diejenigen Werte von , für die diese Tangente eine positive Steigung hat und zudem die x-Achse in einem Punkt schneidet, dessen x-Koordinate größer als ist.
Bestimmen Sie diejenigen Werte von , für die diese Tangente eine positive Steigung hat und zudem die x-Achse in einem Punkt schneidet, dessen x-Koordinate größer als ist.
Gegeben ist die in definierte Funktion mit . Die Abbildung 1 zeigt den Graphen von ohne das zugrunde liegende Koordinatensystem.
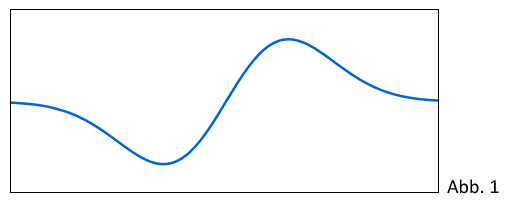

Teilaufgabe Teil B 1a (4 BE)
Zeigen Sie anhand des Funktionsterms von , dass der Graph von symmetrisch bezüglich des Koordinatenursprungs ist. Begründen Sie, dass genau eine Nullstelle hat, und geben Sie den Grenzwert von für .
Teilaufgabe Teil B 1b (2 BE)
Bestimmen Sie einen Term der ersten Ableitungsfunktion von .
(zur Kontrolle: )
(zur Kontrolle: )
Teilaufgabe Teil B 1c (5 BE)
Untersuchen Sie rechnerisch das Monotonieverhalten von . Ergänzen Sie in der Abbildung 1 die Koordinatenachsen und skalieren Sie diese passend.
Teilaufgabe Teil B 1d (3 BE)
Ist die erste Ableitungsfunktion einer in definierten Funktion , so gilt bekanntlich . Berechnen Sie damit den Wert des Terms .
Teilaufgabe Teil B 1e (3 BE)
Interpretieren Sie den folgenden Sachverhalt geometrisch:
Für jede Stammfunktion von und für jede reelle Zahl gilt .
Für jede Stammfunktion von und für jede reelle Zahl gilt .
Betrachtet wird nun die Schar der in definierten Funktionen mit .
Teilaufgabe Teil B 2a (3 BE)
Zeigen Sie, dass genau ein Graph der Schar den Punkt enthält, und geben Sie den zugehörigen Wert von an.
Teilaufgabe Teil B 2b (2 BE)
Der Graph der Funktion ist eine Gerade. Geben Sie die Steigung dieser Gerade und die Koordinaten ihres Schnittpunkts mit der y-Achse an.
Teilaufgabe Teil B 2c (3 BE)
Die folgenden Aussagen gelten für alle reellen Zahlen , und :
-
-
- oder
Geben Sie an, was sich aus diesen Aussagen hinsichtlich des Verlaufs der Graphen der Schar folgern lässt.
-
-
- oder
Geben Sie an, was sich aus diesen Aussagen hinsichtlich des Verlaufs der Graphen der Schar folgern lässt.
Teilaufgabe Teil B 2d (3 BE)
Zeigen Sie, dass die folgende Aussage für jeden Wert von richtig ist:
Wird der Graph von mit dem gleichen Faktor sowohl in x-Richtung als auch in y-Richtung gestreckt, so stellt der dadurch entstehende Graph ebenfalls eine Funktion der Schar dar.
Wird der Graph von mit dem gleichen Faktor sowohl in x-Richtung als auch in y-Richtung gestreckt, so stellt der dadurch entstehende Graph ebenfalls eine Funktion der Schar dar.
Die Graphen der Schar lassen sich in die beiden folgenden Gruppen I und II einteilen:
Der Graph hat genau zwei Extrempunkte.
Der Graph hat keine Extrempunkte.
Die Abbildung 2 zeigt einen Graphen der Gruppe I, die Abbildung 3 einen Graphen der Gruppe II.
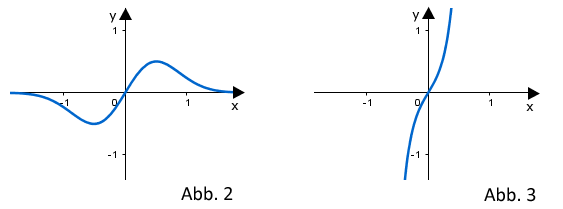
Die Extremstellen von stimmen mit den Lösungen der Gleichung überein.
Der Graph hat genau zwei Extrempunkte.
Der Graph hat keine Extrempunkte.
Die Abbildung 2 zeigt einen Graphen der Gruppe I, die Abbildung 3 einen Graphen der Gruppe II.

Die Extremstellen von stimmen mit den Lösungen der Gleichung überein.
Teilaufgabe Teil B 2e (3 BE)
Geben Sie zu jeder der beiden Gruppen I und II alle zugehörigen Werte von a an und begründen Sie Ihre Angabe.
Teilaufgabe Teil B 2f (3 BE)
Alle Extrempunkte der Graphen der Schar liegen auf einer Gerade.
Begründen Sie, dass es sich dabei um die Gerade mit der Gleichung handelt.
Begründen Sie, dass es sich dabei um die Gerade mit der Gleichung handelt.
Teilaufgabe Teil B 2g (6 BE)
Für jeden positiven Wert von bilden der Hochpunkt des Graphen von , der Punkt , der Koordinatenursprung und der Punkt die Eckpunkte eines Vierecks. Bestimmen Sie ausgehend von einer geeigneten Skizze denjenigen Wert von , für den das Viereck den Flächeninhalt 49 hat.
Lösungen zu:
Tipp:
Arbeite frühzeitig mit der Merkhilfe Mathematik,
die als Hilfsmittel im Abitur zugelassen ist.
die als Hilfsmittel im Abitur zugelassen ist.
Feedback:
Du hast einen Fehler gefunden oder hast Anregungen zur Internetseite?








