über 250 kostenlose
Abituraufgaben
Lösung als Video
und ausformuliert
Alle Lösungen von
erfahrenen Lehrern
Abitur 2022 Mathematik Analytische Geometrie VI
Wird der Punkt an der Ebene gespiegelt, so ergibt sich der Punkt .
Teilaufgabe Teil A a (3 BE)
Bestimmen Sie eine Gleichung von in Koordinatenform.
Teilaufgabe Teil A b (2 BE)
Auf der Gerade durch und liegen die Punkte und symmetrisch bezüglich ; dabei liegt bezüglich auf der gleichen Seite wie . Der Abstand von und ist doppelt so groß wie der Abstand von und .
Bestimmen Sie die Koordinaten von .
Bestimmen Sie die Koordinaten von .
Die Abbildung 1 zeigt das sogenannte Saarpolygon, ein im Inneren begehbares Denkmal zur Erinnerung an den stillgelegten Kohlebergbau im Saarland.
Das Saarpolygon kann in einem Koordinatensystem modellhaft durch den Streckenzug dargestellt werden, der aus den drei Strecken , und mit , , und besteht (vgl. Abbildung 2). , , und sind Eckpunkte eines Quaders. Eine Längeneinheit im Koordinatensystem entspricht einem Meter in der Wirklichkeit.
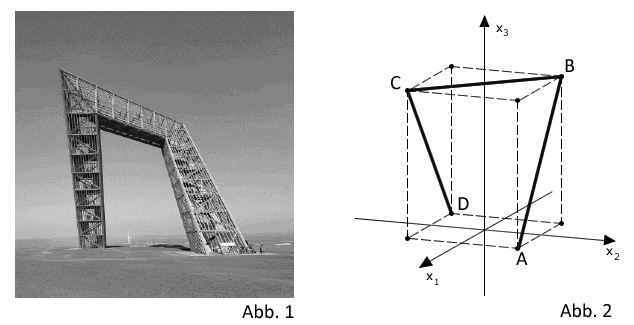
Das Saarpolygon kann in einem Koordinatensystem modellhaft durch den Streckenzug dargestellt werden, der aus den drei Strecken , und mit , , und besteht (vgl. Abbildung 2). , , und sind Eckpunkte eines Quaders. Eine Längeneinheit im Koordinatensystem entspricht einem Meter in der Wirklichkeit.
Teilaufgabe Teil B a (2 BE)
Begründen Sie, dass die Punkte und symmetrisch bezüglich der -Achse liegen.
Teilaufgabe Teil B b (3 BE)
Berechnen Sie die Länge des Streckenzugs in der Wirklichkeit.
Die Ebene enthält die Punkte , und , die Ebene die Punkte , und .
Teilaufgabe Teil B c (4 BE)
Bestimmen Sie eine Gleichung von in Koordinatenform.
(zur Kontrolle: )
(zur Kontrolle: )
Teilaufgabe Teil B d (5 BE)
Berechnen Sie die Größe des Winkels, unter dem die -Ebene schneidet. Geben Sie einen Term an, mit dem aus die Größe des Winkels zwischen den Ebenen und berechnet werden kann.
Teilaufgabe Teil B e (3 BE)
Die Ebene teilt den Quader in zwei Teilkörper. Bestimmen Sie den Anteil des Volumens des pyramidenförmigen Teilkörpers am Volumen des Quaders, ohne die Volumina zu berechnen.
Teilaufgabe Teil B f (4 BE)
Das Saarpolygon wird mit verschiedenen Blickrichtungen betrachtet. Die Abbildungen 3 und 4 stellen das Saarpolygon für zwei Blickrichtungen schematisch dar.
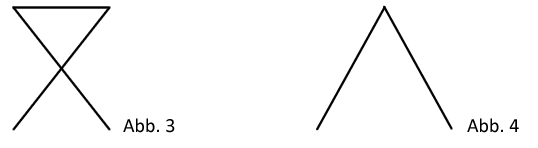
Geben Sie zu jeder der beiden Abbildungen 3 und 4 einen möglichen Vektor an, der die zugehörige Blickrichtung beschreibt. Stellen Sie das Saarpolygon schematisch für eine Betrachtung von oben dar.
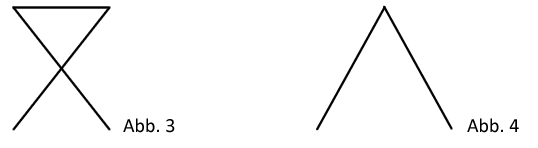
Geben Sie zu jeder der beiden Abbildungen 3 und 4 einen möglichen Vektor an, der die zugehörige Blickrichtung beschreibt. Stellen Sie das Saarpolygon schematisch für eine Betrachtung von oben dar.
Teilaufgabe Teil B g (4 BE)
Der Punkt liegt innerhalb des Quaders und hat von den drei Strecken , und den gleichen Abstand. Das folgende Gleichungssystem liefert den Wert von :
,
Erläutern Sie die Überlegungen, die diesem Vorgehen zur Bestimmung des Werts von zugrunde liegen.
,
Erläutern Sie die Überlegungen, die diesem Vorgehen zur Bestimmung des Werts von zugrunde liegen.
Lösungen zu:
Lösung als Video:
Themen-Übersicht
Tipp:
Arbeite frühzeitig mit der Merkhilfe Mathematik,
die als Hilfsmittel im Abitur zugelassen ist.
die als Hilfsmittel im Abitur zugelassen ist.
Feedback:
Du hast einen Fehler gefunden oder hast Anregungen zur Internetseite?
© 2001 - 2024 Abiturloesung.de. Alle Rechte vorbehalten.
