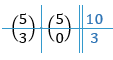Abitur 2021 Mathematik Stochastik IV Aufgabe Teil B 1

über 250 kostenlose

Abituraufgaben

Lösung als Video

und ausformuliert

Alle Lösungen von

erfahrenen Lehrern

Dir gefällt unser
kostenloses Angebot?

Lösung Abitur Bayern 2021 Mathematik Stochastik IV

zur Angabe dieser Abituraufgabe

Teilaufgabe Teil B 1 (3 BE)

Ein Süßwarenunternehmen stellt verschiedene Sorten Fruchtgummis her.

Luisa nimmt an einer Betriebsbesichtigung des Unternehmens teil. Zu Beginn der Führung bekommt sie ein Tütchen mit zehn Gummibärchen, von denen fünf weiß, zwei rot und drei grün sind. Luisa öffnet das Tütchen und nimmt, ohne hinzusehen, drei Gummibärchen heraus. Berechnen Sie die Wahrscheinlichkeit dafür, dass die drei Gummibärchen die gleiche Farbe haben.

Lösung zu Teilaufgabe Teil B 1

Wahrscheinlichkeit

weitere Abituraufgaben zu diesem Thema

5 weiß
2 rot
3 grün

Erläuterung

Nur im Falle von weißen oder grünen Gummibärchen kann der Fall von 3 gleichen Gummibärchen vorkommen.

3 x Weiße Gummibärchen:

Beim 1. Ziehen gibt es 5 weiße Gummibärchen von 10

\Rightarrow

p = \frac{5}{10}

Beim 2. Ziehen gibt es nur noch 4 weiße Gummibärchen von 9 (1 wurde ja bereits gezogen)

\Rightarrow

p = \frac{4}{9}

Beim 3. Ziehen gibt es nur noch 3 weiße Gummibärchen von 8 (2 wurde ja bereits gezogen)

\Rightarrow

p = \frac{3}{8}

\Rightarrow

P ("3 mal weiße Gummibärchen ") = \frac{5}{10} \cdot \frac{4}{9} \cdot \frac{3}{8}

P ("gleiche Farbe") = \underset{3 x weiss}{\underset{︸}{\frac{5}{10} \cdot \frac{4}{9} \cdot \frac{3}{8}}} + \underset{3 x grün}{\underset{︸}{\frac{3}{10} \cdot \frac{2}{9} \cdot \frac{1}{8}}} = \frac{11}{120}

Ziehen ohne Reihenfolge ohne Zurücklegen

weitere Abituraufgaben zu diesem Thema

Alternative Berechnung:

Erläuterung

P ("gleiche Farbe") = \underset{3 x weiss}{\underset{︸}{\frac{(\binom{5}{3}) \cdot \overset{1}{\overset{︷}{(\binom{5}{0})}}}{(\binom{10}{3})}}} + \underset{3 x grün}{\underset{︸}{\frac{(\binom{3}{3}) \cdot \overset{1}{\overset{︷}{(\binom{7}{0})}}}{(\binom{10}{3})}}} + = \frac{(\binom{5}{3}) + (\binom{3}{3})}{(\binom{10}{3})} = \frac{11}{120}

P ("gleiche Farbe") = \frac{(\binom{5}{3}) + (\binom{3}{3})}{(\binom{10}{3})} = \frac{11}{120}

Ziehen ohne Reihenfolge und ohne Zurücklegen

Es handelt sich hier um Ziehen ohne Reihenfolge (welches Gummibärchen wann gezogen wird ist irrelevant) und ohne Zurücklegen (beim gleichzeitigen Ziehen kann ein gezogenes Gummibärchen nicht erneut gezogen werden).

Stichwort: "Lottoprinzip" bzw. hypergeometrische Verteilung:

P (X) = \frac{Anzahl Treffer \cdot Anzahl Nieten}{| Ω |}

3 von 5 weißen Gummibärchen werden gezogen:

\Rightarrow | Treffer | = (\binom{5}{3})

0 von 5 andere Gummibärchen werden gezogen:

\Rightarrow | Niete | = (\binom{5}{0})

3 von insgesamt 10 Gummibärchen werden gewählt:

\Rightarrow | Ω | = (\binom{10}{3})

Merkhilfe zur Kontrolle:

Alle Abituraufgaben

Lösungen zu:

Teilaufgabe Teil A a

Teilaufgabe Teil A b

Teilaufgabe Teil B 1

Teilaufgabe Teil B 2a

Teilaufgabe Teil B 2b

Teilaufgabe Teil B 2c

Teilaufgabe Teil B 3a

Teilaufgabe Teil B 3b

Teilaufgabe Teil B 3c

Teilaufgabe Teil B 4a

Teilaufgabe Teil B 4b

Themen dieser Aufgabe:

Wahrscheinlichkeit

Ziehen ohne Reihenfolge ohne Zurücklegen

Themen-Übersicht

Tipp:

Arbeite frühzeitig mit der Merkhilfe Mathematik,
die als Hilfsmittel im Abitur zugelassen ist.

Feedback:

Du hast einen Fehler gefunden oder hast Anregungen zur Internetseite?

Teile uns Dein Feedback mit!

Abiturloesung.de bei
Facebook