über 250 kostenlose
Abituraufgaben
Lösung als Video
und ausformuliert
Alle Lösungen von
erfahrenen Lehrern

Lösung Abitur Bayern 2020 Mathematik Stochastik IV

zur Angabe dieser Abituraufgabe
Teilaufgabe Teil B 2a  (4 BE)
Neben dem Fußballturnier werden für die Schülerinnen und Schüler auch ein Elfmeterschießen und ein Torwandschießen angeboten.
Dafür konnten sich die Kinder in zwei Listen eintragen. 45 % der Kinder haben sich sowohl für das Torwandschießen als auch für das Elfmeterschießen eingetragen, 15 % haben sich nur für das Elfmeterschießen eingetragen. 90 % der Kinder, die sich für das Torwandschießen eingetragen haben, haben sich auch für das Elfmeterschießen eingetragen. Aus den Kindern wird eines zufällig ausgewählt. Betrachtet werden die folgenden Ereignisse:

T : "Das Kind hat sich für das Torwandschießen eingetragen."
E : "Das Kind hat sich für das Elfmeterschießen eingetragen."
Untersuchen Sie die Ereignisse T und E auf stochastische Unabhängigkeit.
 
Lösung zu Teilaufgabe Teil B 2a
Baumdiagramm erstellen



Text analysieren und Daten herauslesen:

" 45 % der Kinder haben sich sowohl für das Torwandschießen als auch für das Elfmeterschießen eingetragen"
⇒ P ( T ∩ E ) = 45 % = 0 , 45

" 15 % haben sich nur für das Elfmeterschießen eingetragen"
⇒ P ( T ¯ ∩ E ) = 15 % = 0 , 15

" 90 % der Kinder, die sich für das Torwandschießen eingetragen haben, haben sich auch für das Elfmeterschießen eingetragen"
⇒ P T ( E ) = 90 % = 0 , 9


Baumdiagramm zeichnen:
P ( E ) = P ( T ∩ E ) + P ( T ¯ ∩ E ) = 0 , 45 + 0 , 15 = 0 , 6
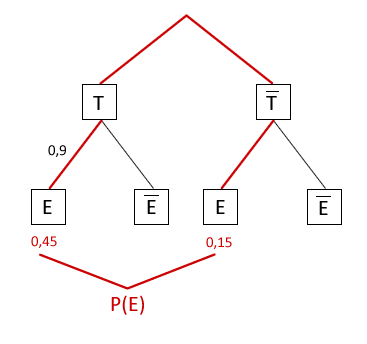
Stochastische Unabhängigkeit



P T ( E ) = 0 , 9 ≠ 0 , 6 = P ( E )
Schritt einblenden / ausblenden
⇒ T und E sind stochastisch abhängig
Alle Abituraufgaben
Lösungen zu:
Teilaufgabe Teil A a
Teilaufgabe Teil A b
Teilaufgabe Teil B 1a
Teilaufgabe Teil B 1b
Teilaufgabe Teil B 2a
Teilaufgabe Teil B 2b
Teilaufgabe Teil B 3a
Teilaufgabe Teil B 3b
Teilaufgabe Teil B 3c
Lösung als Video:
Lösung als Video
Themen dieser Aufgabe:
Baumdiagramm erstellen
Stochastische Unabhängigkeit
Themen-Übersicht
Themen
Tipp:
Arbeite frühzeitig mit der Merkhilfe Mathematik,
die als Hilfsmittel im Abitur zugelassen ist.
Feedback:

Du hast einen Fehler gefunden oder hast Anregungen zur Internetseite?

Teile uns Dein Feedback mit!